题目内容
甲生一般在7：30～7：50到校，乙生一般在7：20～7：55到校，则甲生比乙生早到校的概率是 ．
考点：几何概型
专题：计算题,概率与统计
分析：分别用x，y表示甲，乙到校的时间，再利用平面直角坐标求出事件（x，y）对应的平面区域与甲生比乙生早到校所对应的区域的面积，利用面积比求概率．
解答：
解：用x表示甲到校的时间，y表示乙到校的时间，
则事件（x，y）对应区域为正方形ABCD，如图：
甲生比乙生早到校，即满足条件x＜y，所对应的区域为梯形CDNM，
∴甲生比乙生早到校的概率P=
=
=
．
故答案为：
．
则事件（x，y）对应区域为正方形ABCD，如图：
甲生比乙生早到校，即满足条件x＜y，所对应的区域为梯形CDNM，
∴甲生比乙生早到校的概率P=
| S梯形CDNM |
| S矩形ABCD |
| ||
| 20×35 |
| 3 |
| 7 |
故答案为：
| 3 |
| 7 |
点评：本题考查了几何概型的概率计算，几何概型的概率计算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
边长为1的正六边形ABCDEF中，点P是正六边形内的一点（含边界），则
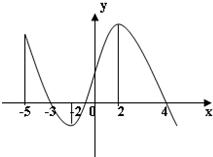如图所示是f′（x）的图象，则正确的判断个数是（ ）（1）f（x）在（-5，-3）上是减函数；
（2）x=4是极大值点；
（3）x=2是极值点；
（4）f（x）在（-2，2）上先减后增．
| A、0 | B、1 | C、2 | D、3 |
数列
，-
，
，-
…的一个通项公式是（ ）
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 7 |
| 16 |
A、an=（-1）n•
| ||
B、an=（-1）n+1•
| ||
C、an=（-1）n•
| ||
D、an=（-1）n+1•
|
如图，在正方体ABCD-A1B1C1D1中，异面直线A1D与D1C所成的角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |