题目内容
在等差数列{an}中,Sn表示前n项和,a1+a6=5,则S6=( )
| A、15 | B、18 | C、12 | D、16 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:直接利用等差数列的前n项和公式求得答案.
解答:
解:在等差数列{an}中,
∵a1+a6=5,
∴S6=
×6=
×6=15.
故选:A.
∵a1+a6=5,
∴S6=
| (a1+a6) |
| 2 |
| 5 |
| 2 |
故选:A.
点评:本题考查等差数列的性质,考查了等差数列的前n项和,是基础题.

练习册系列答案
相关题目
已知函数f(x)=acos(πx+β)+bsin(πx+α),且f(2013)=6,则f(2014)的值是( )
| A、-6 | B、-1 | C、-3 | D、6 |
函数f(x)=
-cosx在(0,+∞)内图象与X轴交点个数( )
| x |
| A、零个 | B、有且仅有一个 |
| C、有且仅有两个 | D、有无穷多个 |
在各项均为正数的数列{an}中,Sn为前n项和,nan+12=(n+1)an2+anan+1,若a2=
,则sinS4=( )
| π |
| 2 |
A、
| ||||||
| B、1 | ||||||
| C、0 | ||||||
D、
|
如图,在正方体ABCD-A1B1C1D1中,异面直线A1D与D1C所成的角为( )


| A、30° | B、45° |
| C、60° | D、90° |
在正方体中,直线A1B与B1C所成的角的大小为( )
| A、30° | B、45° |
| C、60° | D、90° |
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.若sinC+sin(B-A)=sin2A,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
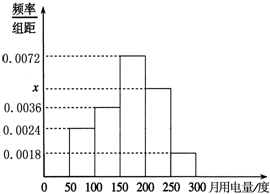 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )