题目内容
函数f(x)=x3-3bx+3b在(0,1)内有极小值的充分不必要条件是( )
| A、b∈(0,1) | ||
| B、b∈(1,+∞) | ||
C、b∈(
| ||
| D、b∈(-∞,1) |
考点:函数在某点取得极值的条件
专题:导数的概念及应用,导数的综合应用
分析:首先求出函数的导数,然后令导数为零,求出函数的极值点,进而求出函数f(x)=x3-3bx+3b在(0,1)内有极小值的充要条件,分析四个答案,与充要条件的包含关系,可得结论.
解答:
解:∵函数f(x)=x3-3bx+3b,
∴f′(x)=3x2-3b,
令f′(x)=0,则x=±
,
若函数f(x)=x3-3bx+3b在(0,1)内有极小值,
则
∈(0,1),即b∈(0,1),
故函数f(x)=x3-3bx+3b在(0,1)内有极小值的充要条件为b∈(0,1),
分析四个答案,
∵(
,1)?(0,1),
故函数f(x)=x3-3bx+3b在(0,1)内有极小值的充分不必要条件可以是b∈(
,1),
故选:C
∴f′(x)=3x2-3b,
令f′(x)=0,则x=±
| b |
若函数f(x)=x3-3bx+3b在(0,1)内有极小值,
则
| b |
故函数f(x)=x3-3bx+3b在(0,1)内有极小值的充要条件为b∈(0,1),
分析四个答案,
∵(
| 1 |
| 2 |
故函数f(x)=x3-3bx+3b在(0,1)内有极小值的充分不必要条件可以是b∈(
| 1 |
| 2 |
故选:C
点评:本题考查的知识点是函数在某点取得极值的条件,充要条件,其中熟练掌握函数在某点取得极值的条件是解答的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
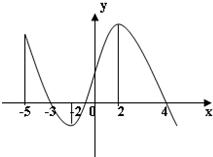 如图所示是f′(x)的图象,则正确的判断个数是( )
如图所示是f′(x)的图象,则正确的判断个数是( )(1)f(x)在(-5,-3)上是减函数;
(2)x=4是极大值点;
(3)x=2是极值点;
(4)f(x)在(-2,2)上先减后增.
| A、0 | B、1 | C、2 | D、3 |
设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列命题,正确的是( )
| A、若m?β,α⊥β,则m⊥α |
| B、若m∥α,m⊥β,则α⊥β |
| C、若α⊥β,α⊥γ,则β⊥γ |
| D、若α∩γ=m,β∩γ=n,m∥n,则α∥β |
数列
,-
,
,-
…的一个通项公式是( )
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 7 |
| 16 |
A、an=(-1)n•
| ||
B、an=(-1)n+1•
| ||
C、an=(-1)n•
| ||
D、an=(-1)n+1•
|
已知函数f(x)=acos(πx+β)+bsin(πx+α),且f(2013)=6,则f(2014)的值是( )
| A、-6 | B、-1 | C、-3 | D、6 |
函数f(x)=
-cosx在(0,+∞)内图象与X轴交点个数( )
| x |
| A、零个 | B、有且仅有一个 |
| C、有且仅有两个 | D、有无穷多个 |
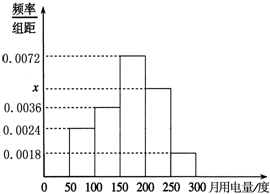 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )