题目内容
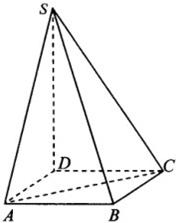 如图,设四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=2a,AD=
如图,设四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=2a,AD=| 2 |
(1)求证:对任意的λ∈(0,2],都有AC⊥BE;
(2)设二面角C-AE-D的大小为θ,直线BE与平面ABCD所成的角为φ,若cosθ=sinφ,求λ的值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的性质
专题:综合题,空间位置关系与距离
分析:(1)因为SD⊥平面ABCD,BD是BE在平面ABCD上的射影,由三垂线定理只要证AC⊥BD即可.
(2)先找出θ和φ,因为由SD⊥平面ABCD知,∠DBE=φ,二面角C-AE-D的平面角可由三垂线定理法作出.再用λ表示出tanθ和tanφ,代入tanθ•tanφ=1,解方程即可.
(2)先找出θ和φ,因为由SD⊥平面ABCD知,∠DBE=φ,二面角C-AE-D的平面角可由三垂线定理法作出.再用λ表示出tanθ和tanφ,代入tanθ•tanφ=1,解方程即可.
解答:
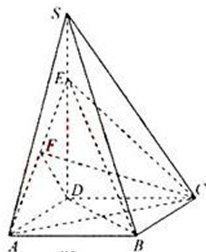 (1)证明:连接BE、BD,由底面ABCD是正方形可得AC⊥BD.
(1)证明:连接BE、BD,由底面ABCD是正方形可得AC⊥BD.
∵SD⊥平面ABCD,∴BD是BE在平面ABCD上的射影,∴AC⊥BE
(2)解:由SD⊥平面ABCD知,∠DBE=φ,
∵SD⊥平面ABCD,CD?平面ABCD,∴SD⊥CD.
又底面ABCD是正方形,∴CD⊥AD,而SD∩AD=D,CD⊥平面SAD.
连接AE、CE,过点D在平面SAD内作DF⊥AE于F,连接CF,则CF⊥AE,
故∠CFD是二面角C-AE-D的平面角,即∠CFD=θ.
在Rt△BDE中,∵BD=2a,DE=λa,
∴tanφ=
=
在Rt△ADE中,∵AD=
a,DE=λa∴AE=a
从而DF=
=
在Rt△CDF中,tanθ=
=
.
由sinφ=cosθ?θ+φ=
?tanθ•tanφ=1,得
•
=1
即
=2,所以λ2=2.
由0<λ≤2,解得λ=
,即为所求.
 (1)证明:连接BE、BD,由底面ABCD是正方形可得AC⊥BD.
(1)证明:连接BE、BD,由底面ABCD是正方形可得AC⊥BD.∵SD⊥平面ABCD,∴BD是BE在平面ABCD上的射影,∴AC⊥BE
(2)解:由SD⊥平面ABCD知,∠DBE=φ,
∵SD⊥平面ABCD,CD?平面ABCD,∴SD⊥CD.
又底面ABCD是正方形,∴CD⊥AD,而SD∩AD=D,CD⊥平面SAD.
连接AE、CE,过点D在平面SAD内作DF⊥AE于F,连接CF,则CF⊥AE,
故∠CFD是二面角C-AE-D的平面角,即∠CFD=θ.
在Rt△BDE中,∵BD=2a,DE=λa,
∴tanφ=
| DE |
| BD |
| λ |
| 2 |
在Rt△ADE中,∵AD=
| 2 |
| λ2+2 |
从而DF=
| AD•DE |
| AE |
| ||
|
在Rt△CDF中,tanθ=
| CD |
| DF |
| ||
| λ |
由sinφ=cosθ?θ+φ=
| π |
| 2 |
| ||
| λ |
| λ |
| 2 |
即
| λ2+2 |
由0<λ≤2,解得λ=
| 2 |
点评:本题考查空间线线垂直的证明、空间垂直之间的相互转化、空间角的求解,考查逻辑推理能力和运算能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列函数,是周期函数的为( )
| A、y=sin|x| |
| B、y=cos|x| |
| C、y=tan|x| |
| D、y=(x-1)0 |
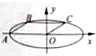 如图,在平面直角坐标系xOy中,点A位椭圆E:
如图,在平面直角坐标系xOy中,点A位椭圆E: