题目内容
18.已知f(x)是定义在[-2,2]上的奇函数,当x∈(0,2]时,f(x)=2x-1,函数g(x)=x2-2x+m,如果对于任意x1∈[-2,2],存在x2∈[-2,2],使得g(x2)=f(x1),则实数m的取值范围是( )| A. | (-∞,-2) | B. | (-5,-2) | C. | [-5,-2] | D. | (-∞,-2] |
分析 求出函数f(x)的值域,根据条件,确定两个函数的最值之间的关系即可得到结论.
解答 解:∵f(x)是定义在[-2,2]上的奇函数,∴f(0)=0,
当x∈(0,2]时,f(x)=2x-1∈(0,3],
则当x∈[-2,2]时,f(x)∈[-3,3],
若对于?x1∈[-2,2],?x2∈[-2,2],使得g(x2)=f(x1),
则等价为g(x)max≥3且g(x)min≤-3,
∵g(x)=x2-2x+m=(x-1)2+m-1,x∈[-2,2],
∴g(x)max=g(-2)=8+m,g(x)min=g(1)=m-1,
则满足8+m≥3且m-1≤-3,
解得m≥-5且m≤-2,
故-5≤m≤-2,
故选C.
点评 本题主要考查函数奇偶性的应用,以及函数最值之间的关系,综合性较强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知a,b是空间两条不同的直线,α,β是两个不同的平面,且a?α,b?β.下列命题正确的是( )
| A. | 若a∥b,且a?β,则α∥β | B. | 若α∥β,则a∥b | ||
| C. | 若a∥b,且a?β,则a∥β | D. | 若a∥β,则a∥b |
6.将直径为2的半圆绕直径所在的直线旋转半周而形成的曲面所围成的几何体的表面积为( )
| A. | 2π | B. | 3π | C. | 4π | D. | 6π |
13.已知F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点.若椭圆C上存在点P,使得线段PF1的中垂线恰好过焦点F2,则椭圆C离心率的取值范围是( )
| A. | [$\frac{2}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{1}{3}$,1) | D. | (0,$\frac{1}{3}$] |
10.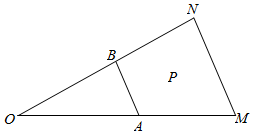 如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
 如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )| A. | [1,2] | B. | [1,4] | C. | $[\frac{1}{2},1]$ | D. | $[\frac{1}{2},4]$ |
7.抛物线y2=4x上一点P到它的焦点F的距离为5,O为坐标原点,则△PFO的面积为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
8.已知a>0,且a≠1,则函数f(x)=ax-1+1的图象恒过定点( )
| A. | (1,1) | B. | (1,2) | C. | (2,1) | D. | (1,0) |