题目内容

4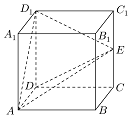．如图，已知正方形ABCD-A1B1C1D1，AA1=2，E为棱CC1的中点，则三棱锥D1-ADE的体积为$\frac{4}{3}$．

分析 由已知求出△DED1的面积，然后利用等体积法求得三棱锥D1-ADE的体积．

解答 解：如图，
∵正方体ABCD-A1B1C1D1的棱AA1=2，E为棱CC1的中点，
∴${S}_{△DE{D}_{1}}=\frac{1}{2}×2×2=2$，
∴${V}_{{D}_{1}-ADE}={V}_{A-DE{D}_{1}}=\frac{1}{3}×2×2=\frac{4}{3}$．
故答案为：$\frac{4}{3}$．

点评 本题考查棱柱、棱锥、棱台的体积的求法，训练了利用等体积法求多面体的体积，是中档题．

练习册系列答案
相关题目
14．我校教育处连续30天对同学们的着装进行检查，着装不合格的人数为如图所示的茎叶图，则中位数，众数，极差分别是（　　）
A．44，45，56B．44，43，57C．44，43，56D．45，43，57
15．设集合M=[0，$\frac{1}{2}$），N=[$\frac{1}{2}$，1]，函数f（x）=$\left\{\begin{array}{l}{x+\frac{1}{2}，x∈M}\\{2（1-x），x∈N}\end{array}\right.$．若x0∈M且f（f（x0））∈M，则x0的取值范围为（　　）
A．（0，$\frac{1}{4}$]B．[0，$\frac{3}{8}$]C．（$\frac{1}{4}$，$\frac{1}{2}$]D．（$\frac{1}{4}$，$\frac{1}{2}$）
12．给定空间中的直线l与平面α，则“直线l与平面α垂直”是“直线l垂直于平面α上无数条直线”的（　　）条件．
A．充分非必要B．必要非充分
C．充要D．既不充分也不必要
19．方程lg（3x+4）=1的解x=2．
9．已知两个不相等的非零向量$\overrightarrow a$和$\overrightarrow b$，向量组$（\overrightarrow{x_1}，\overrightarrow{x_2}，\overrightarrow{x_3}，\overrightarrow{x_4}）$和$（\overrightarrow{y_1}，\overrightarrow{y_2}，\overrightarrow{y_3}，\overrightarrow{y_4}）$均由2个$\overrightarrow a$和2个$\overrightarrow b$排列而成，记$S=\overrightarrow{x_1}•\overrightarrow{y_1}+\overrightarrow{x_2}•\overrightarrow{y_2}+\overrightarrow{x_3}•\overrightarrow{y_3}+\overrightarrow{x_4}•\overrightarrow{y_4}$，那么S的所有可能取值中的最小值是$4\overrightarrow{a}•\overrightarrow{b}$（用向量$\overrightarrow a$、$\overrightarrow b$表示）
16．在平面直角坐标系上，有一点列P0，P1，P2，P3，…，Pn-1，Pn，设点Pk的坐标（xk，yk）（k∈N，k≤n），其中xk、yk∈Z，记△xk=xk-xk-1，△yk=yk-yk-1，且满足|△xk|•|△yk|=2（k∈N*，k≤n）；
（1）已知点P0（0，1），点P1满足△y1＞△x1＞0，求P1的坐标；
（2）已知点P0（0，1），△xk=1（k∈N*，k≤n），且{yk}（k∈N，k≤n）是递增数列，点Pn在直线l：y=3x-8上，求n；
（3）若点P0的坐标为（0，0），y2016=100，求x0+x1+x2+…+x2016的最大值．
13．已知函数$f（x）=\left\{{\begin{array}{l}{2x-5}&{x＜1}\\{x+\frac{a}{x}}&{x≥1}\end{array}}\right.$为R上的单调函数，则实数a的取值范围是[-4，1]．
3．已知函数f（x）=$\frac{{|{{2^x}-1}|}}{{{2^x}+1}}$．
（1）判断函数f（x）的奇偶性；
（2）写出函数的单调区间，并证明函数f（x）在（-∞，0）上的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网