题目内容
3.已知函数f(x)=$\frac{{|{{2^x}-1}|}}{{{2^x}+1}}$.(1)判断函数f(x)的奇偶性;
(2)写出函数的单调区间,并证明函数f(x)在(-∞,0)上的单调性.
分析 (1)计算f(-x)和f(x)的关系,判断函数的奇偶性即可;(2)根据函数单调性的定义判断函数的单调性即可.
解答 解:(1)∵函数f(x)的定义域为R,
且$f({-x})=\frac{{|{{2^{-x}}-1}|}}{{{2^{-x}}+1}}=\frac{{|{1-{2^x}}|}}{{1+{2^x}}}=f(x)$,
所以函数f(x)为偶函数.
(2)函数f(x)的减区间是(-∞,0),增区间是(0,+∞),
x∈(-∞,0)时,f(x)=$\frac{2}{{2}^{x}+1}$-1,
任取x1,x2∈(-∞,0),且x1<x2,
则f(x2)-f(x2)
=$\frac{2}{{2}^{{x}_{2}}+1}$-1-$\frac{2}{{2}^{{x}_{1}}+1}$+1=$\frac{2{(2}^{{x}_{1}}{-2}^{{x}_{2}})}{{(2}^{{x}_{1}}+1){(2}^{{x}_{2}}+1)}$,
∵x1<x2,∴${2^{x_1}}-{2^{x_2}}<0,{2^{x_1}}+1>0,{2^{x_2}}+1>0$,
∴f(x2)-f(x1)<0,
∴f(x2)<f(x1),
∴f(x)为减函数.
点评 本题考查了函数的单调性、奇偶性问题,是一道中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.函数f(x)=cos2x+6sin($\frac{π}{2}$+x)的最大值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
12.已知命题p:函数y=log2($\sqrt{{x}^{2}+1}$-x)是奇函数;命题q:?x0∈(0,+∞),2${\;}^{{x}_{0}}$=$\frac{1}{2}$,则下列判断正确的是( )
| A. | p是假命题 | B. | q是真命题 | C. | p∧(¬q)是真命题 | D. | (¬p)∧q是真命题 |
13.已知集合A={-1,1,2},集合B={x|x-1>0},集合A∩B为( )
| A. | ϕ | B. | {1,2} | C. | {-1,1,2} | D. | {2} |
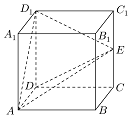 如图,已知正方形ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则三棱锥D1-ADE的体积为$\frac{4}{3}$.
如图,已知正方形ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则三棱锥D1-ADE的体积为$\frac{4}{3}$.