题目内容
求极坐标系中，圆ρ=2上的点到直线ρ（cosθ+
sinθ）=6的距离的最小值．
| 3 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把直线与圆的极坐标方程分别化为直角坐标方程，再利用点到直线的距离公式即可得出．
解答：
解：由 ρ=2即ρ2=4，则x2+y2=4，
由ρ(cosθ+
sinθ)=6，可得x+
y-6=0．
∴圆心（0，0）到直线的距离为d=
=3．
∵圆的半径为2，
∴圆上的点到直线的距离的最小值为d-2=3-2=1．
由ρ(cosθ+
| 3 |
| 3 |
∴圆心（0，0）到直线的距离为d=
| |0+0-6| | ||||
|
∵圆的半径为2，
∴圆上的点到直线的距离的最小值为d-2=3-2=1．
点评：本题考查了把直线与圆的极坐标方程分别化为直角坐标方程、点到直线的距离公式，考查了计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设O为原点，M（2，-1），若点N（x，y）满足不等式组
，则
•
的最小值是（ ）
|
| OM |
| ON |
| A、-3 | B、-2 | C、-1 | D、0 |
已知函数f（x）=
，若|f（x）|≥kx，则k的取值范围是（ ）
|
| A、（-∞，0] |
| B、（-∞，1] |
| C、[-2，1] |
| D、[-2，0] |
一个几何体的三视图是一个正方形，一个矩形，一个半圈，尺寸大小如图所示，则该几何体的表面积是（ ）| A、π | B、3π+4 |
| C、π+4 | D、2π+4 |
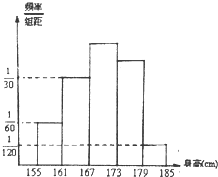某校对高三年级男生的身体发育情况进行调查，共抽取60名男生的身高作为样本，其频率分布直方图如图所示，则身高在[167，179）之间的人数为（ ）