题目内容
16.如图,在四棱锥A-BCD中,△ABD、△BCD均为正三角形,且平面ABD⊥平面BCD,点O,M分别为棱BD,AC的中点,则异面直线AB与OM所成角的余弦值为( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}+\sqrt{6}}}{4}$ |
分析 如图所示,连接OA,OC,取BC的中点E,连接ME,OE,则∠EMO(或其补角)为异面直线AB与OM所成角.利用余弦定理可得结论.
解答 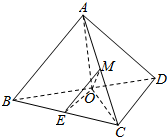 解:如图所示,连接OA,OC,取BC的中点E,连接ME,OE,则
解:如图所示,连接OA,OC,取BC的中点E,连接ME,OE,则
∠EMO(或其补角)为异面直线AB与OM所成角,
∵O为棱BD的中点,
∴OA⊥BD,
∵平面ABD⊥平面BCD,
∴OA⊥平面BCD.
设AB=2,则EM=EO=1,AO=CO=$\sqrt{3}$,∴OM=$\frac{1}{2}$AC=$\frac{\sqrt{6}}{2}$,
∴异面直线AB与OM所成角的余弦值为$\frac{1+\frac{6}{4}-1}{2×1×\frac{\sqrt{6}}{2}}$=$\frac{\sqrt{6}}{4}$.
故选:A.
点评 本题考查空间角,考查学生的计算能力,确定异面直线AB与OM所成角是关键.

练习册系列答案
相关题目
7.已知向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$不共面,则满足A,B,C,P四点共面的条件是( )
| A. | $\overrightarrow{OP}$=2x$\overrightarrow{AO}$+3y$\overrightarrow{BO}$+4z$\overrightarrow{CO}$,且2x+3y+4z=1 | B. | $\overrightarrow{OP}$+$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$ | ||
| C. | $\overrightarrow{AP}$=$\overrightarrow{AB}$+3$\overrightarrow{AC}$ | D. | $\overrightarrow{AP}$=2$\overrightarrow{OB}$-$\overrightarrow{OC}$ |
8.“x>3”是“x>5”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既充分也不必要条件 |