题目内容
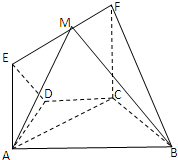 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.(1)求证:平面FBC⊥平面ACFE;
(2)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知条件利用勾股定理求出BC⊥AC.由平面ACFE⊥平面ABCD,得到BC⊥平面ACFE.由此能证明平面ACFE⊥平面FBC.
(2)建立分别以直线CA,CB,CF为x轴,y轴,z轴的空间直角坐标系,令FM=λ(0≤λ≤
),利用向量法能求出cosθ的取值范围.
(2)建立分别以直线CA,CB,CF为x轴,y轴,z轴的空间直角坐标系,令FM=λ(0≤λ≤
| 3 |
解答:
(1)证明:在四边形ABCD中,
∵AB∥CD,AD=DC=CB=1,∠ABC=60°,∴AB=2,
∴AC2=AB2+BC2-2AB•BC•cos60°=3,
∴AB2=AC2+BC2,∴BC⊥AC.
 ∵平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,
∵平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,
BC?平面ABCD,∴BC⊥平面ACFE.
又∵BC?平面FBC,∴平面ACFE⊥平面FBC.…(5分)
(2)解:由(1)可建立分别以直线CA,CB,CF
为x轴,y轴,z轴的如图所示的空间直角坐标系,
令FM=λ(0≤λ≤
),
则C(0,0,0),A(
,0,0),B(0,1,0),M(λ,0,1),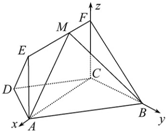
∴
=(-
,1,0),
=(λ,-1,1),
设
=(x,y,z)为平面MAB的一个法向量,
由
,得
取x=1,则
=(1,
,
-λ),
∵
=(1,0,0)是平面FCB的一个法向量,
∴cosθ=cos<
,
>=
=
,…(10分)
∵0≤λ≤
,∴当λ=0时,cosθ有最小值
,
当λ=
时,cosθ有最大值
.
∴cosθ∈[
,
].…(12分)
∵AB∥CD,AD=DC=CB=1,∠ABC=60°,∴AB=2,
∴AC2=AB2+BC2-2AB•BC•cos60°=3,
∴AB2=AC2+BC2,∴BC⊥AC.
 ∵平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,
∵平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,BC?平面ABCD,∴BC⊥平面ACFE.
又∵BC?平面FBC,∴平面ACFE⊥平面FBC.…(5分)
(2)解:由(1)可建立分别以直线CA,CB,CF
为x轴,y轴,z轴的如图所示的空间直角坐标系,
令FM=λ(0≤λ≤
| 3 |
则C(0,0,0),A(
| 3 |

∴
| AB |
| 3 |
| BM |
设
| n |
由
|
|
取x=1,则
| n |
| 3 |
| 3 |
∵
| m |
∴cosθ=cos<
| n |
| m |
| 1 | ||||
|
=
| 1 | ||||
|
∵0≤λ≤
| 3 |
| ||
| 7 |
当λ=
| 3 |
| 1 |
| 2 |
∴cosθ∈[
| ||
| 7 |
| 1 |
| 2 |
点评:本题考查平面与平垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知函数f(x)=
,若f(a)=0,则实数a的值等于( )
|
| A、-3 | B、1 |
| C、-3或1 | D、-1或3 |
F1,F2是椭圆
+
=1(a>b>0)的左、右焦点,若在椭圆上存在点P,且满足|PF1|=2|PF2|,则椭圆的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||
B、(
| ||
C、(
| ||
D、(0,
|
数列{an}满足a1=
,an+1=1-
,那么a10=( )
| 1 |
| 2 |
| 1 |
| an |
| A、-1 | ||
B、
| ||
| C、1 | ||
| D、2 |
圆(x-3)2+y2=4与圆x2+(y-4)2=16的位置关系为( )
| A、内切 | B、外切 | C、相交 | D、相离 |
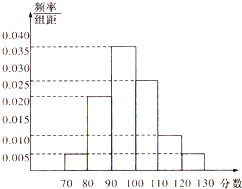 我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.
我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.