题目内容
12.点M(x,y)在|x|+|y|≤2表示的平面区域内,则点M(x,y)满足x+y-1≥0的概率为0.25.分析 首先求出M所在区域的面积以及满足x+y-1≥0的区域面积,利用面积比求概率.
解答 解:由题意点M(x,y)在|x|+|y|≤2表示的平面区域是边长为2$\sqrt{2}$的正方形,面积为8,
点M(x,y)满足x+y-1≥0的区域是长为2$\sqrt{2}$,宽为$\frac{\sqrt{2}}{2}$的矩形,面积为2,
由几何概型的公式得到所求概率为$\frac{2}{8}$=0.25;
故答案为:0.25
点评 本题考查了几何概型的概率求法;关键是明确几何测度.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
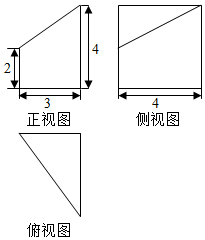
3. 已知某几何体的三视图如图所示,则该几何体的表面积为( )
已知某几何体的三视图如图所示,则该几何体的表面积为( )
 已知某几何体的三视图如图所示,则该几何体的表面积为( )
已知某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 16+3π | B. | 12+3π | C. | 8+4$\sqrt{2}$+3π | D. | 4+4$\sqrt{2}$+3π |
20.设命题p:存在两个相交平面垂直于同一条直线;命题q:?x∈R,x2-2x+1≥0.则下 列命题为真命题的是( )
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
17.执行如图所示的程序框图,若x∈[a,b],y∈[0,4],则b-a的最小值为( )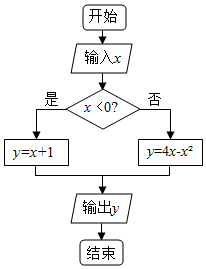

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.已知命题P:?α∈R,sinα+cosα≤$\sqrt{2}$,则( )
| A. | ¬p:?α∈R,sinα+cosα≥$\sqrt{2}$ | B. | ¬p:?α∈R,sinα+cosα≥$\sqrt{2}$ | ||
| C. | ¬p:?α∈R,sinα+cosα>$\sqrt{2}$ | D. | ¬p:?α∈R,sinα+cosα>$\sqrt{2}$ |
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,F1、F2是椭圆的左、右焦点,点A为椭圆的右顶点,点B为椭圆的上顶点,且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,F1、F2是椭圆的左、右焦点,点A为椭圆的右顶点,点B为椭圆的上顶点,且S${\;}_{△AB{F}_{1}}$=$\frac{\sqrt{2}+1}{2}$.