题目内容
1.已知命题P:?α∈R,sinα+cosα≤$\sqrt{2}$,则( )| A. | ¬p:?α∈R,sinα+cosα≥$\sqrt{2}$ | B. | ¬p:?α∈R,sinα+cosα≥$\sqrt{2}$ | ||
| C. | ¬p:?α∈R,sinα+cosα>$\sqrt{2}$ | D. | ¬p:?α∈R,sinα+cosα>$\sqrt{2}$ |
分析 利用全称命题的否定是特称命题,去判断.
解答 解:因为命题是全称命题,根据全称命题的否定是特称命题,
所以命题的否定:¬p:?α∈R,sinα+cosα>$\sqrt{2}$.
故选:C
点评 本题主要考查全称命题的否定,要求掌握全称命题的否定是特称命题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.设a、b、c是正实数,则“a、b、c依次成等差数列”是“$b≥\sqrt{ac}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.求函数f(x)=x+$\frac{1}{x}$-1-ln(x+3)零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
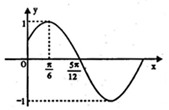 已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示.
已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示.