题目内容
20.设命题p:存在两个相交平面垂直于同一条直线;命题q:?x∈R,x2-2x+1≥0.则下 列命题为真命题的是( )| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
分析 本题的关键是判定命题p;命题q这两个命题的真假,再利用复合命题的真假判定.
解答 解:对于命题p:存在两个相交平面垂直于同一条直线
显然p是假命题,则¬p是真命题;
对于命题q:?x∈R,x2-2x+1=(x-1)2≥0.是真命题;
∴根据复合命题真假判定,
A:(1)p∧q是假命题
B:p∧(¬q)是假命题
C:(¬p)∧(¬q)是假命题
D:(¬p)∧q是真命题
故选:D.
点评 本题考查的知识点是复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.

练习册系列答案
相关题目
10.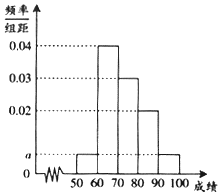 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;
(3)若这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示,求数学成绩在[50,90)之外的人数.(分数可以不为整数)
 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x::y | 1:1 | 2:1 | 3:4 | 4:5 |
(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;
(3)若这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示,求数学成绩在[50,90)之外的人数.(分数可以不为整数)
15.已知椭圆E:$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的一个顶点为C(0,-2),直线l与椭圆E交于A、B两点,若E的左焦点为△ABC的重心,则直线l的方程为( )
| A. | 6x-5y-14=0 | B. | 6x-5y+14=0 | C. | 6x+5y+14=0 | D. | 6x+5y-14=0 |
9.设a、b、c是正实数,则“a、b、c依次成等差数列”是“$b≥\sqrt{ac}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.求函数f(x)=x+$\frac{1}{x}$-1-ln(x+3)零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |