题目内容
18.命题“任意x∈R,x2>0”的否定是存在x0∈R,x02≤0.分析 直接利用全称命题的否定是特称命题写出结果即可.
解答 解:因为全称命题的否定是特称命题,
所以命题“对任意的x∈R,x2>0”的否定是:存在x0∈R,x02≤0.
故答案为:存在x0∈R,x02≤0.
点评 本题考查命题的否定,特称命题与全称命题的否定关系.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3.正四棱锥P-ABCD的侧棱长为$\sqrt{5}$,底面ABCD边长为2,E为AD的中点,则BD与PE所成角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
10.已知矩形ABCD中,AB=6,BC=4,E,F分别是AB,CD上两动点,且AE=DF,把四边形BCFE沿EF折起,使平面BCFE⊥平面ABCD,若折得的几何体的体积最大,则该几何体外接球的体积为( )
| A. | 28π | B. | $\frac{{28\sqrt{7}π}}{3}$ | C. | 32π | D. | $\frac{{64\sqrt{2}π}}{3}$ |
7.要得到y=cos2x-1的图象,只需将函数y=sin2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| C. | 向右平移$\frac{π}{2}$个单位,再向上平移1个单位 | |
| D. | 向左平移$\frac{π}{2}$个单位,再向下平移1个单位 |
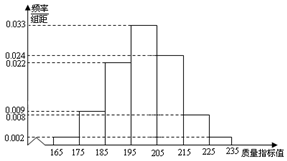 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).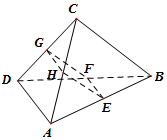 (理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC
(理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC