题目内容
设集合M={x|x2-mx+6=0，x∈R}且M∪{2，3}={2，3}，则实数m的取值范围是 ．
考点：交集及其运算
专题：集合
分析：由M∪{2，3}={2，3}，得到M为{2，3}的子集，即2或3为M中方程的解，求出M的值，即可得到满足题意m的范围．
解答：
解：∵M∪{2，3}={2，3}，
∴M⊆{2，3}，
当M=∅时，M中方程无解，即△=m2-24＜0，
解得：-2
＜m＜2
，
当m≠∅时，把x=2代入方程得：4-2m+6=0，即m=5，
把x=3代入方程得：9-3m+6=0，即m=5，
综上，m的范围为{m|m=5或-2
＜m＜2
}．
故答案为：{m|m=5或-2
＜m＜2
}
∴M⊆{2，3}，
当M=∅时，M中方程无解，即△=m2-24＜0，
解得：-2
| 6 |
| 6 |
当m≠∅时，把x=2代入方程得：4-2m+6=0，即m=5，
把x=3代入方程得：9-3m+6=0，即m=5，
综上，m的范围为{m|m=5或-2
| 6 |
| 6 |
故答案为：{m|m=5或-2
| 6 |
| 6 |
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
已知复数z满足（1-i）z=2，则|
|为（ ）
. |
| z |
| A、1+i | ||
| B、1-i | ||
C、
| ||
| D、2 |
若全集U={-1，-2，-3，-4}，M={-2，-3}，则∁UM（ ）
| A、{-1，-2，-3} |
| B、{-2} |
| C、{-4} |
| D、{-1，-4} |
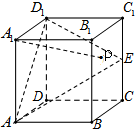如图所示，在长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，AA1=3，E是棱CC1上的点，且| CE |
| 1 |
| 3 |
| CC1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
化（
） -
的结果是（ ）
| 27 |
| 125 |
| 1 |
| 3 |
| A、3 | ||
| B、5 | ||
C、
| ||
D、
|