题目内容
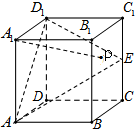 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,AA1=3,E是棱CC1上的点,且
如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,AA1=3,E是棱CC1上的点,且| CE |
| 1 |
| 3 |
| CC1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:直线与平面所成的角
专题:计算题,向量法,空间位置关系与距离,空间角
分析:以B为原点,BA,BC,BB1所在直线为x,y,z轴,建立空间直角坐标系,设P(0,s,t),求得A1,A,E,D1,B1的坐标,连接B1P,则由A1B1⊥平面BCC1B1所,则∠A1PB1即为A1P与平面BCC1B1所成角,则tan∠A1PB1=
,要求最大值,只要求B1P的最小值,设平面D1AE的法向量为
=(x,y,z),由向量垂直的条件,求出法向量,再由
⊥
,求出P的轨迹方程,即为直线,再由点到直线的距离公式,即可得到.
| A1B1 |
| B1P |
| n |
| n |
| A1P |
解答:
 解:以B为原点,BA,BC,BB1所在直线为x,y,z轴,建立空间直角坐标系,
解:以B为原点,BA,BC,BB1所在直线为x,y,z轴,建立空间直角坐标系,
设P(0,s,t),且A1(2,0,3),A(2,0,0),E(0,2,1),D1(2,2,3),B1(0,0,3),
连接B1P,则由A1B1⊥平面BCC1B1所,则∠A1PB1即为A1P与平面BCC1B1所成角,
则tan∠A1PB1=
,
=(-2,2,1),
=(0,2,3),
=(-2,s,t-3),
设平面D1AE的法向量为
=(x,y,z),
则
⊥
,即
•
=0,即有-2x+2y+2z=0,
⊥
,即有2y+3z=0,即y=-
z,x=-z,
可取
=(-2,-3,2),由于A1P∥面D1AE,则
⊥
,
即有
•
=0,即4-3s+2(t-3)=0,即2t-3s-2=0,
则B1P的最小值为d=
=
,
则tan∠A1PB1的最大值为:
=
.
故选C.
 解:以B为原点,BA,BC,BB1所在直线为x,y,z轴,建立空间直角坐标系,
解:以B为原点,BA,BC,BB1所在直线为x,y,z轴,建立空间直角坐标系,设P(0,s,t),且A1(2,0,3),A(2,0,0),E(0,2,1),D1(2,2,3),B1(0,0,3),
连接B1P,则由A1B1⊥平面BCC1B1所,则∠A1PB1即为A1P与平面BCC1B1所成角,
则tan∠A1PB1=
| A1B1 |
| B1P |
| AE |
| AD1 |
| A1P |
设平面D1AE的法向量为
| n |
则
| n |
| AE |
| n |
| AE |
| n |
| AD1 |
| 3 |
| 2 |
可取
| n |
| n |
| A1P |
即有
| n |
| A1P |
则B1P的最小值为d=
| |2×3-2| | ||
|
| 4 | ||
|
则tan∠A1PB1的最大值为:
| 2 | ||||
|
| ||
| 2 |
故选C.
点评:本题考查空间直线和平面所成的角的求法,考查坐标法求空间角,考查空间直线与平面的位置关系,考查运算能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=
如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中不正确的是( )
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AB∥平面ABC |
设f(x)=|xex|,若关于x的方程(1-t)f2(x)-f(x)+t=0有四个不同的实数根,则实数t的取值范围为( )
| A、(-∞,0) | ||
B、(0,
| ||
C、(
| ||
| D、(1,+∞) |
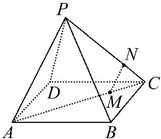 如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )
如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )| A、MN∥PD |
| B、MN∥PA |
| C、MN∥AD |
| D、以上均有可能 |
