题目内容
△ABC的三个顶点在平面α的同侧,所在平面不与α平行,AA′⊥α于A′,BB′⊥α于B′,CC′⊥α于C′,G、G′分别为△ABC和△A′B′C′的重心.
(1)求证:GG′⊥α;
(2)若AA′=a,BB′=b,CC′=c,求GG′的长.
(1)求证:GG′⊥α;
(2)若AA′=a,BB′=b,CC′=c,求GG′的长.
考点:点、线、面间的距离计算,直线与平面垂直的性质
专题:计算题,空间位置关系与距离
分析:(1)取AC的中点D,A'C'的中点为D',连接DD',由重心的性质和线面垂直的性质,即可得证;
(2)运用梯形的中位线定理,以及三等分点公式,即可得到GG'.
(2)运用梯形的中位线定理,以及三等分点公式,即可得到GG'.
解答:
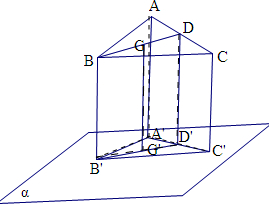 (1)证明:取AC的中点D,A'C'的中点为D',
(1)证明:取AC的中点D,A'C'的中点为D',
连接DD',则DD'∥BB',
由于G,G'分别为重心,则
=
=2,
则GG'∥BB',
由于BB′⊥α,则GG′⊥α;
(2)解:由于AA′=a,BB′=b,CC′=c,
则DD'=
,
即有GG'=
=
.
 (1)证明:取AC的中点D,A'C'的中点为D',
(1)证明:取AC的中点D,A'C'的中点为D',连接DD',则DD'∥BB',
由于G,G'分别为重心,则
| BG |
| GD |
| B′G′ |
| G′D′ |
则GG'∥BB',
由于BB′⊥α,则GG′⊥α;
(2)解:由于AA′=a,BB′=b,CC′=c,
则DD'=
| a+c |
| 2 |
即有GG'=
b+2×
| ||
| 1+2 |
| a+b+c |
| 3 |
点评:本题考查空间直线与平面的位置关系,考查线面垂直的性质定理,考查点到平面的距离,考查三角形的重心的性质,属于中档题.

练习册系列答案
相关题目
函数y=
+
是( )
| 1-|x| |
| 9 |
| 1+x2 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |