题目内容
在公差不为零的等差数列{an}中，a1=8-a3，且a4为a2和a9的等比中项，求数列{an}的首项、公差及前n项和．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用a1=8-a3，且a4为a2和a9的等比中项，建立方程，求出首项为1，公差为3，即可求出数列的前n项和．
解答：
解：设该数列公差为d（d≠0），前n项和为Sn．
由已知，可得 2a1+2d=8，(a1+3d)2=(a1+d)(a1+8d)．（4分）
所以a1+d=4，d（d-3a1）=0，
解得，a1=1，d=3，（8分）
即数列{an}的首项为1，公差为3．（10分）
所以数列的前n项和Sn=
（12分）
由已知，可得 2a1+2d=8，(a1+3d)2=(a1+d)(a1+8d)．（4分）
所以a1+d=4，d（d-3a1）=0，
解得，a1=1，d=3，（8分）
即数列{an}的首项为1，公差为3．（10分）
所以数列的前n项和Sn=
| 3n2-n |
| 2 |
点评：基本量法是解决数列问题的首选方法．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
定义域为R的四个函数y=x2+1，y=3x，y=|x+1|，y=sinx中，偶函数的个数是（ ）
| A、4 | B、3 | C、2 | D、1 |
已知命题P：复数z=
在复平面内所对应的点位于第四象限；命题q：?x＞0，x=cosx，则下列命题中为真命题的是（ ）
| 1+i |
| i |
| A、（￢p）∧（￢q） |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、p∧q |
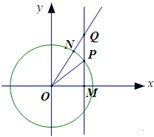在直角坐标系xOy中，点p是单位圆上位于第一象限的动点，过p作x轴的垂线与射线y=xtanθ（x≥0，0＜θ＜