题目内容
若存在实数x0与正数a,使x0+a,x0-a均在函数f(x)的定义域内,且f(x0+a)=f(x0-a)成立,则称“函数f(x)在x=x0处存在长度为a的对称点”.
(1)设f(x)=x3-3x2+2x-1,问是否存在正数a,使“函数f(x)在x=1处存在长度为a的对称点”?试说明理由.
(2)设g(x)=x+
(x>0),若对于任意x0∈(3,4),总存在正数a,使得“函数g(x)在x=x0处存在长度为a的对称点”,求b的取值范围.
(1)设f(x)=x3-3x2+2x-1,问是否存在正数a,使“函数f(x)在x=1处存在长度为a的对称点”?试说明理由.
(2)设g(x)=x+
| b |
| x |
考点:奇偶函数图象的对称性
专题:计算题,函数的性质及应用
分析:(1)由f(1+a)=f(1-a)得(1+a)3-3(1+a)2+2(1+a)-1=(1-a)3-3(1-a)2+2(1-a)-1,化简即可求出正数a;
(2)令g(x)=c,则x+
=c,即x2-cx+b=0必须有两正根,且两根的算术平均数为x0,即可求b的取值范围.
(2)令g(x)=c,则x+
| b |
| x |
解答:
解:(1)∵f(1+a)=f(1-a),
∴(1+a)3-3(1+a)2+2(1+a)-1=(1-a)3-3(1-a)2+2(1-a)-1,
∴a(a+1)(a-1)=0,
∵a>0,
∴a=1;
(2)令g(x)=c,则x+
=c,即x2-cx+b=0(*).
由题意,方程(*)必须有两正根,且两根的算术平均数为x0,
∴c>0,b>0,c2-4b>0,
=x0,
∴0<b<x02对一切意x0∈(3,4)均成立,
∴b的取值范围为(0,9].
∴(1+a)3-3(1+a)2+2(1+a)-1=(1-a)3-3(1-a)2+2(1-a)-1,
∴a(a+1)(a-1)=0,
∵a>0,
∴a=1;
(2)令g(x)=c,则x+
| b |
| x |
由题意,方程(*)必须有两正根,且两根的算术平均数为x0,
∴c>0,b>0,c2-4b>0,
| c |
| 2 |
∴0<b<x02对一切意x0∈(3,4)均成立,
∴b的取值范围为(0,9].
点评:本题考查新定义,考查函数的性质,考查学生的计算能力,正确理解新定义是关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
在平面直角坐标系中,已知三点A(m,n),B(n,t),C(t,m),直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为
,而直线AB恰好经过抛物线x2=2p(y-q),(p>0)的焦点F并且与抛物线交于P、Q两点(P在y轴左侧).则|
|=( )
| 5 |
| 3 |
| PF |
| QF |
| A、9 | ||||
| B、4 | ||||
C、
| ||||
D、
|
执行如图所示的程序框图,如果输入a=2,那么输出的结果为( )


| A、2 | B、3 | C、4 | D、5 |
 已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为
已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为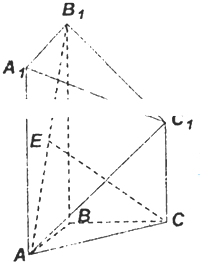 如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点.
如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点.