题目内容
王师傅驾车去超市,途中要经过4个路口,假设在各路口遇到红灯的概率都是
,遇到红灯时,在各路口停留的时间依次为30秒,30秒,60秒,30秒
(Ⅰ)求王师傅在第3个路口首次遇到红灯的概率;
(Ⅱ)求王师傅在途中因遇到红灯停留的总时间X(秒)的分布列及数学期望.
| 1 |
| 3 |
(Ⅰ)求王师傅在第3个路口首次遇到红灯的概率;
(Ⅱ)求王师傅在途中因遇到红灯停留的总时间X(秒)的分布列及数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(Ⅰ)王师傅在第3个路口首次遇到红灯,则前2个路口没有遇到红灯,故可求概率;
(Ⅱ)X=0,30,60,90,120,150,求出随机变量取每一个值的概率值,即可求X的分布列及其数学期望EX.
(Ⅱ)X=0,30,60,90,120,150,求出随机变量取每一个值的概率值,即可求X的分布列及其数学期望EX.
解答:
解:(Ⅰ)设“王师傅在第3个路口首次遇到红灯”为事件A,则
P(A)=(1-
)2×
=
;
(Ⅱ)X=0,30,60,90,120,150,则
P(X=0)=(1-
)4=
,P(X=30)=
×
×(1-
)3=
,
P(X=60)=
×(
)2×(1-
)2+(1-
)3×
=
,
P(X=90)=(
)3×(1-
)+
×(
)2×(1-
)2=
,
P(X=120)=
×(1-
)×(
)3=
,
P(X=150)=(
)4=
,
X的分布列为
数学期望EX=0×
+30×
+60×
+90×
+120×
+150×
=50.
P(A)=(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
(Ⅱ)X=0,30,60,90,120,150,则
P(X=0)=(1-
| 1 |
| 3 |
| 16 |
| 81 |
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
P(X=60)=
| C | 2 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 20 |
| 81 |
P(X=90)=(
| 1 |
| 3 |
| 1 |
| 3 |
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 14 |
| 81 |
P(X=120)=
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
P(X=150)=(
| 1 |
| 3 |
| 1 |
| 81 |
X的分布列为
| X | 0 | 30 | 60 | 90 | 120 | 150 | ||||||||||||
| P |
|
|
|
|
|
|
| 16 |
| 81 |
| 8 |
| 27 |
| 20 |
| 81 |
| 14 |
| 81 |
| 2 |
| 27 |
| 1 |
| 81 |
点评:求随机变量的分布列与期望的关键是确定变量的取值,求出随机变量取每一个值的概率值.

练习册系列答案
相关题目
已知回归直线的斜率的估计值是2,样本点的中心为(4,12),则回归直线的方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个四面体的四个顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,2,0),(0,2,2),(3,0,1),则该四面体中以yOz平面为投影面的正视图的面积为( )
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
执行如图所示的程序框图,如果输入a=2,那么输出的结果为( )


| A、2 | B、3 | C、4 | D、5 |

 已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为
已知圆E的圆心在x轴上,且与y轴切于原点.过抛物线y2=2px(p>0)焦点F作垂直于x轴的直线l分别交圆和抛物线于A、B两点.已知l截圆所得的弦长为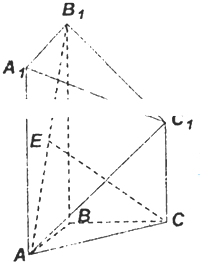 如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点.
如图,在几何体ABC-A1B1C1中,点A1、B1、C1在平面ABC内的正投影分别为A、B、C,且AB⊥BC,AA1=BB1=4,AB=BC=CC1=2,E为AB1的中点.