题目内容
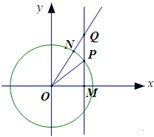 在直角坐标系xOy中,点p是单位圆上位于第一象限的动点,过p作x轴的垂线与射线y=xtanθ(x≥0,0<θ<
在直角坐标系xOy中,点p是单位圆上位于第一象限的动点,过p作x轴的垂线与射线y=xtanθ(x≥0,0<θ<| π |
| 2 |
(1)若θ=
| π |
| 3 |
| 3 |
| 5 |
(2)若θ=
| π |
| 4 |
(3)并求取最大值时的α值.
考点:三角函数中的恒等变换应用,任意角的三角函数的定义
专题:三角函数的求值
分析:(1)由题意求出sinα和cosα的值,再根据cos∠POQ=cos(
-α).利用两角差的余弦公式计算求得结果.
(2)根据SOMPN=S△OMP+S△OPN=
cosαsinα+
(sinα-cosα).令sinα-cosα=t,根据 SOMPN=-
(t-
)2+
,利用二次函数的性质求得四边形OMPN面积的最大值.
(3)由(2)可得t=
时,SOMPN 有最大值
,此时,cos(α+
)=
,根据α+
的范围,可得α的值.
| π |
| 3 |
(2)根据SOMPN=S△OMP+S△OPN=
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| 3 |
| 8 |
(3)由(2)可得t=
| ||
| 2 |
| 3 |
| 8 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
解答:
 解:(1)由题意,∠MOQ=
解:(1)由题意,∠MOQ=
,∠POQ=∠MOQ-∠MOP=
-α,
∵sinα=
,α∈(0,
),∴cosα=
.
所以cos∠POQ=cos(
-α)=cos
cosα+sin
sinα=
.
(2)∵SOMPN=S△OMP+S△OPN=
cosαsinα+
sin(
-α)
=
cosαsinα+
(cosα-sinα).
令cosα-sinα=t,∵α∈(0,
),则t∈(0,1),
∴SOMPN=
(1-t2)-
t=-
(t-
)2+
,
当t=
时,SOMPN 有最大值
.
(3)当SOMPN 有最大值时,cosα-sinα=
,有cos(α+
)=
,由于α+
∈(
,
),
所以 α=
为所求.
 解:(1)由题意,∠MOQ=
解:(1)由题意,∠MOQ=| π |
| 3 |
| π |
| 3 |
∵sinα=
| 3 |
| 5 |
| π |
| 2 |
| 4 |
| 5 |
所以cos∠POQ=cos(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
4+3
| ||
| 10 |
(2)∵SOMPN=S△OMP+S△OPN=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
=
| 1 |
| 2 |
| ||
| 4 |
令cosα-sinα=t,∵α∈(0,
| π |
| 4 |
∴SOMPN=
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| 3 |
| 8 |
当t=
| ||
| 2 |
| 3 |
| 8 |
(3)当SOMPN 有最大值时,cosα-sinα=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
所以 α=
| π |
| 12 |
点评:本题主要考查任意角的三角函数的定义,三角函数的恒等变换及化简求值,二次函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
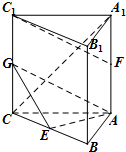 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AB=AA1,E、F分别是棱BC,A1A的中点,G为棱CC1上的一点,且C1F∥平面AEG.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AB=AA1,E、F分别是棱BC,A1A的中点,G为棱CC1上的一点,且C1F∥平面AEG.