题目内容
已知函数f(x)=a|x+1|-b|2x-4|,当a=1,b=
时,解不等式f(x)≤0.
| 1 |
| 2 |
考点:绝对值不等式的解法
专题:计算题,分类讨论,不等式的解法及应用
分析:首先求出f(x)=|x+1|-|x-2|,不等式f(x)≤0即为|x+1|≤|x-2|,运用平方法化简不等式,即可得到解集.
解答:
解:当a=1,b=
时,f(x)=|x+1|-
|2x-4|=|x+1|-|x-2|,
不等式f(x)≤0即为|x+1|-|x-2|≤0,
即|x+1|≤|x-2|,
两边平方可得x2+2x+1≤x2-4x+4,
即6x-3≤0,
解得x≤
.
则解集为(-∞,
].
| 1 |
| 2 |
| 1 |
| 2 |
不等式f(x)≤0即为|x+1|-|x-2|≤0,
即|x+1|≤|x-2|,
两边平方可得x2+2x+1≤x2-4x+4,
即6x-3≤0,
解得x≤
| 1 |
| 2 |
则解集为(-∞,
| 1 |
| 2 |
点评:本题考查绝对值不等式的解法,考查运算能力,运用平方法是解题的关键.

练习册系列答案
相关题目
曲线
+
=1与曲线
+
=1(0<k<9)具有( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、相等的长、短轴 |
| B、相等的焦距 |
| C、相等的离心率 |
| D、相同的准线 |
10件产品中有3件次品,不放回地抽取2次,在第1次抽出的是次品的前提下,则第2次抽出正品的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
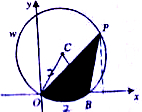 如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴正半轴于点B(2,0),P是弧OwB上的一个动点,且∠OPB=30°,设P点坐标为(m,n).
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴正半轴于点B(2,0),P是弧OwB上的一个动点,且∠OPB=30°,设P点坐标为(m,n).