题目内容
已知等比数列{an}的前n项和为Sn,a1=1,且S2+
a2=4.
(1)求数列{an}的通项公式;
(2)记bn=an•log2an,求数列{bn}的前n项和Tn.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)记bn=an•log2an,求数列{bn}的前n项和Tn.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)设等比数列{an}的公比为q,利用等比数列的通项公式及其前n项和定义即可得出.
(2)bn=an•log2an=(n-1)•2n-1,利用“错位相减法”、等比数列的前n项和公式即可得出.
(2)bn=an•log2an=(n-1)•2n-1,利用“错位相减法”、等比数列的前n项和公式即可得出.
解答:
解:(1)设等比数列{an}的公比为q,
∵a1=1,且S2+
a2=4,
∴1+q+
q=4,解得q=2,
∴an=2n-1.
(2)bn=an•log2an=(n-1)•2n-1,
∴数列{bn}的前n项和Tn=0+2+2×22+3×23+…+(n-1)×2n-1,
2Tn=0+22+2×23+3×24+…+(n-2)×2n-1+(n-1)×2n,
∴-Tn=2+22+23+…+2n-1-(n-1)×2n=
-(n-1)×2n=(2-n)×2n-2,
∴Tn=(n-2)×2n+2.
∵a1=1,且S2+
| 1 |
| 2 |
∴1+q+
| 1 |
| 2 |
∴an=2n-1.
(2)bn=an•log2an=(n-1)•2n-1,
∴数列{bn}的前n项和Tn=0+2+2×22+3×23+…+(n-1)×2n-1,
2Tn=0+22+2×23+3×24+…+(n-2)×2n-1+(n-1)×2n,
∴-Tn=2+22+23+…+2n-1-(n-1)×2n=
| 2(2n-1-1) |
| 2-1 |
∴Tn=(n-2)×2n+2.
点评:本题考查了等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知圆锥的母线长为5cm,圆锥的侧面展开图如图所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.则蚂蚁爬行的最短路程长为( ) 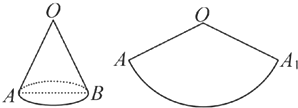

| A、8 cm | ||
B、5
| ||
| C、10 cm | ||
| D、5πcm |
若
sinα+sin(
-α)=
,则sin(
+2α)的值为( )
| 3 |
| 3π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
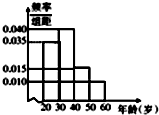 某学校有120名教师,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分组,其频率分布直方图如右图所示.学校为了适应新课程改革,要求每名教师都要参加甲、乙两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响.
某学校有120名教师,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分组,其频率分布直方图如右图所示.学校为了适应新课程改革,要求每名教师都要参加甲、乙两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响.