题目内容
若对一切x∈R,不等式4x+(a-1)2x+1≥0恒成立,则a的取值范围是 .
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:把不等式4x+(a-1)2x+1≥0变形得到a≥-2x-
+1,令2x=t(t>0)换元后构造函数g(t)=-t-
+1(t>0),由导数求其最大值后得答案.
| 1 |
| 2x |
| 1 |
| t |
解答:
解:当x∈R时,2x>0,
∴不等式4x+(a-1)2x+1≥0恒成立等价于a-1≥
=-2x-
恒成立,
即a≥-2x-
+1恒成立.
令2x=t(t>0).
即a≥-t-
+1(t>0)恒成立.
令g(t)=-t-
+1(t>0),
g′(t)=-1+
=
,
当t∈(0,1)时,g′(t)>0,
当t∈(1,+∞)时,g′(t)<0.
∴当t=1时g(t)有极大值也就是最大值,
g(t)max=g(1)=-1.
∴a≥-1.
故答案为:a≥-1.
∴不等式4x+(a-1)2x+1≥0恒成立等价于a-1≥
| -4x-1 |
| 2x |
| 1 |
| 2x |
即a≥-2x-
| 1 |
| 2x |
令2x=t(t>0).
即a≥-t-
| 1 |
| t |
令g(t)=-t-
| 1 |
| t |
g′(t)=-1+
| 1 |
| t2 |
| -t2+1 |
| t2 |
当t∈(0,1)时,g′(t)>0,
当t∈(1,+∞)时,g′(t)<0.
∴当t=1时g(t)有极大值也就是最大值,
g(t)max=g(1)=-1.
∴a≥-1.
故答案为:a≥-1.
点评:本题考查了恒成立问题,考查了换元法和函数构造法,训练了利用导数求函数的最值,是中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
在等比数列{an}中,a1=27,a4=a3a5,则a6=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
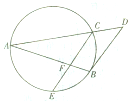 如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且
如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且