题目内容
(x+
)6的展开式中的常数项等于 .
| 1 |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答:
解:(x+
)6的展开式的通项公式为 Tr+1=
•x6-2r,
令6-2r=0,求得 r=3,∴展开式中的常数项等于
=20,
故答案为:20.
| 1 |
| x |
| C | r 6 |
令6-2r=0,求得 r=3,∴展开式中的常数项等于
| C | 3 6 |
故答案为:20.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
设f(x)是定义在R上的偶函数,?x∈R,都有f(2-x)=f(2+x),且当x∈[0,2]时,f(x)=2x-2,若函数g(x)=f(x)-loga(x+1)(a>0,a≠1)在区间(-1,9]内恰有三个不同零点,则实数a的取值范围是( )
A、(0,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
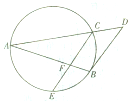 如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且
如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且