题目内容
若f(x+2)=
,则f(
+2)•f(-14)= .
|
| 21π |
| 4 |
考点:函数的周期性
专题:函数的性质及应用
分析:由函数的解析式可得分别求得f(
+2)=-
,f(-14)=4,相乘可得.
| 21π |
| 4 |
| ||
| 2 |
解答:
解:由题意可得f(
+2)=sin
=sin(6π-
)=-sin
=-
,
同理可得f(-14)=f(-16+2)=log216=4,
∴f(
+2)•f(-14)=-
×4=-2
,
故答案为:-2
| 21π |
| 4 |
| 21π |
| 4 |
=sin(6π-
| 3π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
同理可得f(-14)=f(-16+2)=log216=4,
∴f(
| 21π |
| 4 |
| ||
| 2 |
| 2 |
故答案为:-2
| 2 |
点评:本题考查函数的周期性,涉及三角函数和对数函数的运算,属基础题.

练习册系列答案
相关题目
在梯形ABCD中,AB∥DC,AD⊥AB,AB=2AD=2DC=4,点N是CD边上一动点,则
•
的最大值为( )
| AN |
| AB |
A、4
| ||
| B、8 | ||
C、8
| ||
| D、16 |
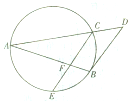 如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且
如图,已知AB、AC、CE是圆的弦,过点B作圆的切线与AC的延长线相交于点D,且