题目内容
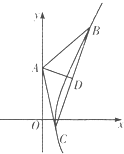 如图,B,C两点在双曲线x2-
如图,B,C两点在双曲线x2-| y2 |
| 4 |
| 7 |
| 15 |
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:确定D的坐标,求出BC,AD,利用韦达定理及弦长公式,即可得出结论.
解答:
解:设BC的斜率为k,B(x1,y1),C(x2,y2),D(x0,y0),
∵B,C两点在双曲线x2-
=1的右支上,
∴kOD=
=
=
,
直线AD的方程为y=-
x+4,可得D(
,
),
∴AD=
,
令∠BAD=α,∵cos∠BAC=-
,∴cosα=
,tanα=
.
∴BC=
又y=kx-
+
代入到双曲线方程可得4x2-(kx-
+
)2=4
即(4-k2)x2-2k(-
+
)x-(-
+
)2-4=0
∴x1+x2=
k,x1x2=
又BC=
∴
=
,
∴20k2-180=0,
∴k2=9
∴AD=
.
故答案为:
.
∵B,C两点在双曲线x2-
| y2 |
| 4 |
∴kOD=
| y1+y2 |
| x1+x2 |
| 4(x1-x2) |
| y1-y2 |
| 4 |
| k |
直线AD的方程为y=-
| 1 |
| k |
| 4k |
| 5 |
| 16 |
| 5 |
∴AD=
| 4 |
| 5 |
| k2+1 |
令∠BAD=α,∵cos∠BAC=-
| 7 |
| 15 |
2
| ||
| 15 |
| ||
| 2 |
∴BC=
4
| ||
| 5 |
| k2+1 |
又y=kx-
| 4k2 |
| 5 |
| 16 |
| 5 |
| 4k2 |
| 5 |
| 16 |
| 5 |
即(4-k2)x2-2k(-
| 4k2 |
| 5 |
| 16 |
| 5 |
| 4k2 |
| 5 |
| 16 |
| 5 |
∴x1+x2=
| 8 |
| 5 |
| -16k4+128k2-356 |
| 25(4-k2) |
又BC=
4
| ||
| 5 |
| k2+1 |
∴
| -16k4+128k2-356 |
| 25(4-k2) |
| 16k2-44 |
| 25 |
∴20k2-180=0,
∴k2=9
∴AD=
4
| ||
| 5 |
故答案为:
4
| ||
| 5 |
点评:本题考查直线与双曲线的位置关系,考查韦达定理的运用,考查学生的计算能力,有难度.

练习册系列答案
相关题目
下列函数中,周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(2x+
| ||||
C、f(x)=2sin(
| ||||
D、f(x)=2sin(2x-
|
设a>0,b>0则下列不等中不恒成立的是( )
A、a+
| ||||||
| B、a2+b2≥2(a+b-1) | ||||||
C、
| ||||||
| D、a3+b3≥2ab2 |