题目内容
12.对于同一平面的单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,若$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,则($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{c}$)的最大值是$\frac{5}{2}$.分析 设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=(cosα,-sinα),代入计算得到($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{c}$)=$\frac{1}{2}$+2sin(α-30°),根据三角函数的性质可求.
解答 解:∵单位向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,
设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=(cosα,-sinα),
∴$\overrightarrow{a}$-$\overrightarrow{b}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{a}$-2$\overrightarrow{c}$=(1-2cosα,-2sinα),
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{c}$)=$\frac{1}{2}$-cosα+$\sqrt{3}$sinα=$\frac{1}{2}$+2sin(α-30°),
∵-1≤sin(α-30°)≤1,
∴-$\frac{3}{2}$≤$\frac{1}{2}$+2sin(α-30°)≤$\frac{5}{2}$,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{c}$)的最大值是$\frac{5}{2}$.
故答案为:$\frac{5}{2}$
点评 本题考查平面向量数量积的运算,函数与方程思想,是中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案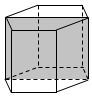 如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )
如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )| A. | $\frac{{3\sqrt{3}}}{4}$m3 | B. | $\frac{3}{4}$m3 | C. | 1m3 | D. | $\frac{1}{2}$m3 |
| A. | [-1,1] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) |
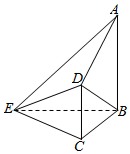 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.