题目内容
17.已知集合A={x|2x2-5x-3≤0},B={x∈Z|x≤2},则A∩B中的元素个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 求出A中不等式的解集确定出A,再由B,求出两集合的交集,即可做出判断.
解答 解:由A中不等式变形得:(2x+1)(x-3)≤0,
解得:-$\frac{1}{2}$≤x≤3,即A={x|-$\frac{1}{2}$≤x≤3},
∵B={x∈Z|x≤2}={2,1,0,-1,…},
∴A∩B={0,1,2},即有3个元素,
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
7.已知变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≤0\\ x≥1\\ x+y-7≤0\end{array}\right.$,则$\frac{x+y}{y}$的取值范围是( )
| A. | $(-∞,\frac{7}{6}]$ | B. | $[\frac{14}{9},+∞)$ | C. | $[\frac{14}{9},7]$ | D. | $[\frac{7}{6},\frac{14}{9}]$ |
6.设P(x,y)满足约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x+y≤3}\end{array}\right.$,则点P对应的区域与坐标轴围成的封闭图形面积为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{11}{2}$ |
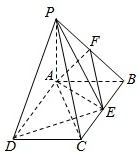 如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.
如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.