题目内容
2.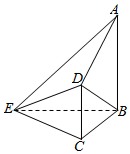 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.(1)求证:平面ADE⊥平面ABE;
(2)求三棱锥A-BDE的体积.
分析 (1)取BE中点O,AE中点F,则可证四边形OCDF是矩形,得出DF⊥OF,再由OC⊥BE,DF∥OC得出DF⊥BE,故而DF⊥平面ABE,于是平面ADE⊥平面ABE;
(2)过E作EG⊥BC,交BC延长线于G,则EG⊥平面ABD,将△ABD当做棱锥底面,则EG为棱锥的高,代入体积公式计算.
解答 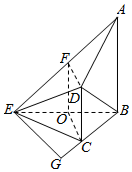 (1)证明:取BE中点O,AE中点F,连结OC,OF,DF,则OF$\stackrel{∥}{=}\frac{1}{2}AB$.
(1)证明:取BE中点O,AE中点F,连结OC,OF,DF,则OF$\stackrel{∥}{=}\frac{1}{2}AB$.
∵AB⊥平面BCE,CD⊥平面BCE,AB=2CD
∴CD$\stackrel{∥}{=}$$\frac{1}{2}$AB,
∴CD$\stackrel{∥}{=}OF$.又∵AB⊥平面BCE,
∴四边形OCDF是矩形.
∴DF⊥OF,DF∥OC,
∵BC=CE,O是BE中点,
∴OC⊥BE,
∴DF⊥BE,又OF?平面ABE,BE?平面ABE,OF∩BE=O,
∴DF⊥平面ABE,∵DF?平面ADE,
∴平面ADE⊥平面ABE.
(2)过E作EG⊥BC,交BC延长线于G,
∵AB⊥平面BCE,EG?平面BCE,
∴EG⊥AB,又AB?平面ABCD,BC?平面ABCD,AB∩BC=B,
∴EG⊥平面ABCD.
∵CE=2,∠BCE=$\frac{2π}{3}$,∴EG=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∵S△ABD=$\frac{1}{2}AB×BC=\frac{1}{2}×2×2$=2,
∴三棱锥A-BDE的体积V=$\frac{1}{3}{S}_{△ABD}×EG$=$\frac{1}{3}×2×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了线面垂直,面面垂直的性质与判定,棱锥的体积计算,找到棱锥的高是解题的关键.

| A. | y=sinx在第三象限内是增函数 | B. | 函数y=sinx(x∈R)的值域是(-1,1) | ||
| C. | y=cosx在x=2kπ(k∈Z)时取值最大 | D. | y=tanx在整个定义域内都是增函数 |
| A. | (-∞,4) | B. | (0,4) | C. | ($\frac{1}{4}$,4) | D. | (4,+∞) |
| A. | $(-∞,\frac{7}{6}]$ | B. | $[\frac{14}{9},+∞)$ | C. | $[\frac{14}{9},7]$ | D. | $[\frac{7}{6},\frac{14}{9}]$ |
| A. | ?x∉R,x2≠x | B. | ?x∈R,x2=x | C. | ?x0∈R,x${\;}_{0}^{2}$≠x0 | D. | ?x0∈R,x${\;}_{0}^{2}$=x0 |
| A. | 公差为5的等差数列 | B. | 公差为6的等差数列 | ||
| C. | 公比为6的等比数列 | D. | 公比为8的等比数列 |