题目内容
20.若函数f(x)=(k2+1)lnx-x2在区间(1,+∞)上是减函数,则实数k的取值范围是( )| A. | [-1,1] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) |
分析 根据f(x)在(1,+∞)上是减函数便得到导数$f′(x)=\frac{{k}^{2}+1}{x}-2x≤0$,从而得到k2+1≤2x2,而可求得2x2>2,从而有k2+1≤2,解该不等式即可得出实数k的取值范围.
解答 解:f(x)在(1,+∞)上是减函数;
∴$f′(x)=\frac{{k}^{2}+1}{x}-2x≤0$;
∴k2+1≤2x2;
∵x∈(1,+∞);
∴2x2>2;
∴k2+1≤2;
∴-1≤k≤1;
∴实数k的取值范围是[-1,1].
故选A.
点评 考查函数单调性和函数导数符号的关系,可根据二次函数y=2x2在(1,+∞)上的单调性得出2x2>2,以及一元二次不等式的解法,注意正确求导.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
3.设正数x,y满足-1<x-y<2,则z=2x-2y的取值范围为( )
| A. | (-∞,4) | B. | (0,4) | C. | ($\frac{1}{4}$,4) | D. | (4,+∞) |
11.已知数列{an}是公比为2的等比数列,数列{bn}是公差为3且各项均为正整数的等差数列,则数列{a${\;}_{{b}_{n}}$}是( )
| A. | 公差为5的等差数列 | B. | 公差为6的等差数列 | ||
| C. | 公比为6的等比数列 | D. | 公比为8的等比数列 |
15.已知复数Z的共轭复数$\overline{Z}$=$\frac{1-i}{1+2i}$,则复数Z的虚部是( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{5}$i | C. | -$\frac{3}{5}$ | D. | -$\frac{3}{5}$i |
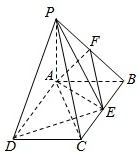 如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.
如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.