题目内容

若函数f（x）=
ax，x＞1
(4-
a
2
)x+2，x≤1
是R上的增函数，则实数a的取值范围为（　　）
A、（1，+∞）
B、（1，8）
C、[4，8）
D、（4，8）
考点：函数单调性的性质,分段函数的应用
专题：函数的性质及应用
分析：让两段都单调递增，且让x=1时ax≥（4-
a
2
）x+2，解关于a的不等式组可得．
解答： 解：∵函数f（x）=
ax，x＞1
(4-
a
2
)x+2，x≤1
是R上的增函数，
∴
a＞1
4-
a
2
＞0
a1≥4-
a
2
+2
，解得4≤a＜8
故选：C
点评：本题考查分段函数的单调性，涉及指数函数和一次函数的单调性，属中档题．
练习册系列答案
相关题目
函数f（x）=（1+x-
x2
2
+
x3
3
-
x4
4
+…-
x2012
2012
+
x2013
2013
）•sin2x在区间[-3，3]上的零点的个数为（　　）
A、3B、4C、5D、6
过已知圆x2+y2-x+2y+
1
4
=0的圆心，且与直线x+y+1=0垂直的直线的一般方程为
 
．
在四边形ABCD中，
AB
=
DC
=（1，1），
BA
|
BA
|
+
BC
|
BC
|
=
3
•
BD
|
BD
|
，则四边形ABCD的面积是
 
．
计算：（sin
π
2
-π）0+1g2+1g5=
 
．
函数f（x）=||2x-1|-2x|的单调递减区间为
 
．
下列“若p，则q”形式的命题中：
①若x∈E或x∈F，则x∈E∪F；
②若关于x的不等式ax2-2ax+a+3＞0的解集为R，则a＞0；
③若
2
x是有理数，
则x是无理数p是q的充分而不必要条件的有
 
个．
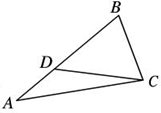如图，D是△ABC的边AB的三等分点，则向量
CD
等于（　　）
A、
CA
+
2
3
AB
B、
CA
+
1
3
AB
C、
CB
+
2
3
AB
D、
CB
+
1
3
AB
已知在xoy平面内有一区域M，命题甲：点（a，b）∈{（x，y||x-1|+|y-2|＜2）}；命题乙：点（a，b）∈M，如果甲是乙的必要条件，那么区域M的面积有（　　）
A、最小值8B、最大值8
C、最小值4D、最大值4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网