题目内容
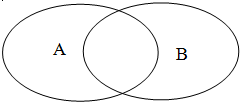 已知A={x|
已知A={x|| 1 |
| 2 |
(1)求A∩B和A∪B;
(2)若记符号A-B={x|x∈A,且x∉B},①在图中把表示“集合A-B”的部分用阴影涂黑;②求A-B和B-A.
考点:Venn图表达集合的关系及运算,交、并、补集的混合运算
专题:集合
分析:(1)求出集合A,B,根据集合的基本运算即可求A∩B和A∪B;
(2)根据定义即可得到结论.
(2)根据定义即可得到结论.
解答:
解:(1)A={x|
<2x<4}={x|-1<x<2},B={x|x-1>0}={x|x>1},
则A∩B={x|1<x<2},A∪B={x|x>-1};
(2)∵A-B={x|x∈A,且x∉B},
∴对应的集合图象为 :
:
②A-B={x|x∈A,且x∉B}={x|-1<x≤1},
B-A={x|x∈B,且x∉A}={x|x≥2}.
| 1 |
| 2 |
则A∩B={x|1<x<2},A∪B={x|x>-1};
(2)∵A-B={x|x∈A,且x∉B},
∴对应的集合图象为
 :
:②A-B={x|x∈A,且x∉B}={x|-1<x≤1},
B-A={x|x∈B,且x∉A}={x|x≥2}.
点评:本题主要考查集合的基本运算,根据定义以及求出集合是解决本题的关键.

练习册系列答案
相关题目
下列命题中,正确的命题是( )
| A、分别在两个不同平面内的两条直线一定是异面直线 |
| B、直线a在α内,直线b不在α内,则a、b是异面直线 |
| C、在空间中,经过直线外一点,有且只有一条直线和这条直线平行 |
| D、垂直于同一条直线的两条直线平行 |
幂函数f(x)=(m2-m-5)xm+1在(0,+∞)上单调递减,则m等于( )
| A、3 | B、-2 | C、-2或3 | D、-3 |
P={(x,y)|x+y=5,x∈N*,y∈N*},则集合的非空子集的个数是( )
| A、3 | B、4 | C、15 | D、16 |
下列各数中最小的数为( )
| A、111111(2) |
| B、210(6) |
| C、1000(4) |
| D、71(8) |
集合A={y|y=
},B={y|y=x2+2},则A∩B表示的集合为( )
| x+1 |
| A、{x|x≥1} |
| B、{x|x≥2} |
| C、{x|1≤x≤2} |
| D、{x|1≤x<2} |
若直线(m+2)x+3y+3=0与直线x+(2m-1)y+m=0平行,则实数m=( )
A、-
| ||
| B、1 | ||
| C、1或2 | ||
D、-
|