题目内容
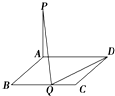 如图,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,BC边上存在点Q,使得PQ⊥QD,则实数a的取值范围是
如图,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,BC边上存在点Q,使得PQ⊥QD,则实数a的取值范围是考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:连接AQ,由已知中PA⊥平面ABCD,四边形ABCD为矩形,我们易得PQ⊥QD?AQ⊥QD,由此我们易得以AD为半径的圆与BC应该有交点,再由AB=1,BC=a,即可得到满足条件的实数a的取值范围.
解答:
解:连接AQ,∵PA⊥平面ABCD,
∴PA⊥QD,若PQ⊥QD成立,
即AQ⊥QD成立,
∴点Q应为BC与以AB为直径的圆的公共点,
∴
≥1,
故满足条件的实数a的取值范围为a≥2;
故答案为:[2,+∞).
∴PA⊥QD,若PQ⊥QD成立,
即AQ⊥QD成立,
∴点Q应为BC与以AB为直径的圆的公共点,
∴
| a |
| 2 |
故满足条件的实数a的取值范围为a≥2;
故答案为:[2,+∞).
点评:本题考查的知识点是直线与平面垂直的性质,解题的关键是将AQ⊥QD转化为BC与以AB为直径的圆的公共点,属于基本知识的考查.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
函数y=ln(x+2)的定义域是( )
| A、(-2,+∞) |
| B、[-2,+∞) |
| C、(2,+∞) |
| D、(0,+∞) |
已知m,n是两条直线,α,β是两个平面,有以下命题:
①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
②若m∥α,m∥β,则α∥β;
③若m∥α,n∥β,m∥n,则α∥β.
其中正确命题的个数是( )
①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;
②若m∥α,m∥β,则α∥β;
③若m∥α,n∥β,m∥n,则α∥β.
其中正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
在△ABC中,|
|=3,|
|=2,点D满足2
=3
,∠BAC=60°,则
•
=( )
| AB |
| AC |
| BD |
| DC |
| AD |
| BC |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA上,且HA1=1.点E,F分别为棱B1C,C1C的中点,P是侧面BCC1B1内一动点,且满足PE⊥PF.则当点P运动时,|HP|2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA上,且HA1=1.点E,F分别为棱B1C,C1C的中点,P是侧面BCC1B1内一动点,且满足PE⊥PF.则当点P运动时,|HP|2的最小值是( )A、7-
| ||
B、27-6
| ||
C、51-14
| ||
D、14-2
|

 如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个结论:
如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个结论: