题目内容
已知函数f(x)=sin(x-
)+cosx.
(1)求函数f(x)的最小正周期;
(2)若α是第一象限角,且f(α+
)=
,求tan(α-
)的值.
| π |
| 6 |
(1)求函数f(x)的最小正周期;
(2)若α是第一象限角,且f(α+
| π |
| 3 |
| 4 |
| 5 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先对三角函数关系式进行恒等变换,把函数关系式变形成正弦型函数,进一步求出函数的最小正周期.
(2)利用(1)求出的函数关系式,进一步求出函数的正弦值和余弦值,进一步求出函数的正切值,最后求出结果.
(2)利用(1)求出的函数关系式,进一步求出函数的正弦值和余弦值,进一步求出函数的正切值,最后求出结果.
解答:
解:(1)f(x)=sin(x-
)+cosx
=
sinx-
cosx+cosx
=
sinx+
cosx
=sin(x+
)
所以:函数f(x)的最小正周期为:T=
=2π
(2)由于f(x)=sin(x+
)
则:f(α+
)=sin(α+
)=cosα=
由于α是第一象限角
所以:sinα=
则:tanα=
则:tan(α-
)=
=-
| π |
| 6 |
=
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(x+
| π |
| 6 |
所以:函数f(x)的最小正周期为:T=
| 2π |
| 1 |
(2)由于f(x)=sin(x+
| π |
| 6 |
则:f(α+
| π |
| 3 |
| π |
| 2 |
| 4 |
| 5 |
由于α是第一象限角
所以:sinα=
| 3 |
| 5 |
则:tanα=
| 3 |
| 4 |
则:tan(α-
| π |
| 4 |
| tanα-1 |
| 1+tanα |
| 1 |
| 7 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的周期的应用,三角函数的求值问题,属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
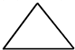
若一个正四棱锥的左视图是一个边长为2的正三角形(如图),则该正四棱锥的体积是( )

| A、1 | ||||
B、
| ||||
C、
| ||||
D、2
|
如图,正六边形ABCDEF中,AB=2,则(
-
)•(
+
)=( )

| BC |
| BA |
| AF |
| BC |

| A、-6 | ||
B、-2
| ||
C、2
| ||
| D、6 |
F是双曲线C:
-
=1(a>0,b>0)的右焦点,过点F向C的一条渐近线引垂线,垂足为 A,交另一条渐近线于点 B.若2
=
,则C的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
若向量
,
不共线,则下列各组向量中,可以作为一组基底的是( )
| a |
| b |
A、
| ||||||||||||
B、3
| ||||||||||||
C、
| ||||||||||||
D、2
|
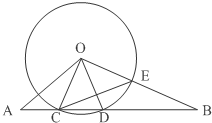 如图,⊙O的半径为6,线段AB与⊙相交于点C、D,AC=4,∠BOD=∠A,OB与⊙O相交于点.
如图,⊙O的半径为6,线段AB与⊙相交于点C、D,AC=4,∠BOD=∠A,OB与⊙O相交于点.