题目内容
在区间[-3，2]上随机选取一个数x，使得函数y=
有意义的概率为（ ）
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：本题符合几何概型，所以分别求出区域的长度，利用几何概型公式解答．
解答：
解：在区间[-3，2]上随机选取一个数x，区间长度为5，
y=
的定义域为：{x|x≥-1}，在区间[-3，2]上满足条件的区间长度为3，
由几何概型公式可得，P=
；
故选：C．
y=
| x+1 |
由几何概型公式可得，P=
| 3 |
| 5 |
故选：C．
点评：本题考查了几何概型概率公式的运用；明确测度，求区间的长度是关键．
练习册系列答案
相关题目
在△ABC中，角A，B，C的对边分别为a，b，c，且满足（2a-c）cosB=bcosC，则B=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
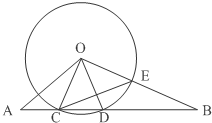如图，⊙O的半径为6，线段AB与⊙相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点．