题目内容
在直角坐标系xOy中,已知曲线C1的参数方程是
(α是参数).现以原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)写出曲线C1的极坐标方程;
(2)曲线C2的极坐标方程是ρ=2,求曲线C2与曲线C1的交点的极坐标.
|
(1)写出曲线C1的极坐标方程;
(2)曲线C2的极坐标方程是ρ=2,求曲线C2与曲线C1的交点的极坐标.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)利用sin2α+cos2α=1消去参数α,即可得出直角坐标方程,把x=ρcosθ,y=ρsinθ,代入即可得出.
(2)分别化为直角坐标方程,联立即可解出.
(2)分别化为直角坐标方程,联立即可解出.
解答:
解 (1)曲线C1的普通方程为:x2+(y-2)2=4 ①
令 x=ρcosθ,y=ρsinθ,
代入直角方程可得:(ρcosθ)2+(ρsinθ-2)2=4,
整理得ρ=4sinθ.
(2)曲线C2的普通方程为:x2+y2=4 ②.
①-②得曲线C1与曲线C2的公共弦所在的直线方程 y=1.
将y=1 代入②得 x=±
,
∴交点坐标为(-
,1 ) (
,1).
其极坐标为 ( 2,
π)或 (2,
).
令 x=ρcosθ,y=ρsinθ,
代入直角方程可得:(ρcosθ)2+(ρsinθ-2)2=4,
整理得ρ=4sinθ.
(2)曲线C2的普通方程为:x2+y2=4 ②.
①-②得曲线C1与曲线C2的公共弦所在的直线方程 y=1.
将y=1 代入②得 x=±
| 3 |
∴交点坐标为(-
| 3 |
| 3 |
其极坐标为 ( 2,
| 5 |
| 6 |
| π |
| 6 |
点评:本题考查了极坐标方程与直角坐标方程的互化、两个圆相交弦长,考查了计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
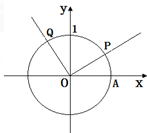 设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,
设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,
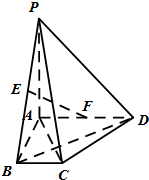 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=PA=2,E,F分别为PB,AD的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=PA=2,E,F分别为PB,AD的中点.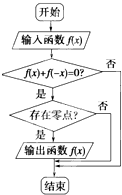 某程序框图如图所示,现输入四个函数(1)f(x)=x2,(2)f(x)=
某程序框图如图所示,现输入四个函数(1)f(x)=x2,(2)f(x)=