题目内容
已知函数f(x)=loga
(其中a>0且a≠1),
(1)求f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)写出函数f(x)的单调区间(不必写出证明过程).
| x-1 |
| x+1 |
(1)求f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)写出函数f(x)的单调区间(不必写出证明过程).
考点:函数单调性的判断与证明,函数的定义域及其求法,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)根据对数函数的真数大于0,求出f(x)的定义域;
(2)根据函数奇偶性的定义,判断f(x)是奇函数;
(3)讨论a>1和1>a>0时,f(x)的增减性即可.
(2)根据函数奇偶性的定义,判断f(x)是奇函数;
(3)讨论a>1和1>a>0时,f(x)的增减性即可.
解答:
解:(1)∵函数f(x)=loga
(a>0且a≠1),
∴
>0,
解答x>1,或x<-1;
∴f(x)的定义域是(-∞,-1)∪(1,+∞);
(2)∵f(x)的定义域是(-∞,-1)∪(1,+∞),
则对定义域内的x,都有
f(-x)=loga
=loga
=-loga
=-f(x),
∴f(x)是定义域上的奇函数;
(3)当a>1时,f(x)在区间(-∞,-1),和(1,+∞)上是增函数;
当1>a>0时,f(x)在区间(-∞,-1),和(1,+∞)上是减函数;
∴a>1时,f(x)的增区间是(-∞,-1),(1,+∞);
1>a>0时,f(x)的减区间是(-∞,-1),(1,+∞).
| x-1 |
| x+1 |
∴
| x-1 |
| x+1 |
解答x>1,或x<-1;
∴f(x)的定义域是(-∞,-1)∪(1,+∞);
(2)∵f(x)的定义域是(-∞,-1)∪(1,+∞),
则对定义域内的x,都有
f(-x)=loga
| -x-1 |
| -x+1 |
| x+1 |
| x-1 |
| x-1 |
| x+1 |
∴f(x)是定义域上的奇函数;
(3)当a>1时,f(x)在区间(-∞,-1),和(1,+∞)上是增函数;
当1>a>0时,f(x)在区间(-∞,-1),和(1,+∞)上是减函数;
∴a>1时,f(x)的增区间是(-∞,-1),(1,+∞);
1>a>0时,f(x)的减区间是(-∞,-1),(1,+∞).
点评:本题考查了对数函数的图象与性质的应用问题,也考查了函数的单调性与奇偶性的判断问题,是基础题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 求函数y=
求函数y=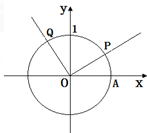 设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,
设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,