题目内容
已知公差不为0的等差数列{an}的首项为2,且a1,a2,a4成等比数列.
(1)求数列{an}的通项公式.
(2)令bn=
,(n∈N+),求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式.
(2)令bn=
| 1 |
| (an+1)2-1 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)利用等差数列及等比数列的性质列出方程求得公差d,即可得出结论;
(2)bn=
=
=
(
-
),利用裂项相消法求和即可.
(2)bn=
| 1 |
| (an+1)2-1 |
| 1 |
| (2n+1)2-1 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)设等差数列{an}的公差为d,由a1,a2,a4成等比数列得
(a2)2=a1•a4,
又a1=2,∴(a1+d)2=a1(a1+3d),
∵d≠0,∴d=2,
∴an=2n.
(2)∵bn=
=
=
(
-
),
∴sn=
(1-
+
-
+…+
-
)=
(1-
)=
.
(a2)2=a1•a4,
又a1=2,∴(a1+d)2=a1(a1+3d),
∵d≠0,∴d=2,
∴an=2n.
(2)∵bn=
| 1 |
| (an+1)2-1 |
| 1 |
| (2n+1)2-1 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴sn=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 4 |
| 1 |
| n+1 |
| n |
| 4(n+1) |
点评:本题主要考查等差数列及等比数列的性质和裂项相消法求和等知识,考查学生的计算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,在△ABC中,BC=1,AB=2,∠ABC=60°,四边形ACDE为矩形,且平面ACDE⊥平面ABC,DC=1.
如图,在△ABC中,BC=1,AB=2,∠ABC=60°,四边形ACDE为矩形,且平面ACDE⊥平面ABC,DC=1. 已知函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<
已知函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|< 求函数y=
求函数y=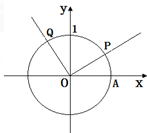 设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,
设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,