题目内容
已知数列{an}的通项公式为an=
,求数列{an}的前n项和Sn.
| 1 |
| (2n+1)(2n+3) |
考点:数列的求和
专题:等差数列与等比数列
分析:由an=
=
(
-
),利用裂项相消法即可求得前n项和.
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
解答:
解:∵an=
=
(
-
),
∴sn=
(
-
+
-
+…+
-
)=
(
-
)=
.
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
∴sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+3 |
| n |
| 3(2n+3) |
点评:本题主要考查利用裂项相消法求数列的前n项和知识,属基础题.

练习册系列答案
相关题目
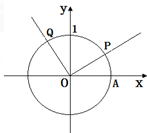 设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,
设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,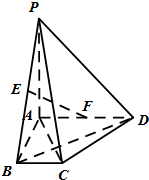 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=PA=2,E,F分别为PB,AD的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=PA=2,E,F分别为PB,AD的中点.