题目内容
4.对于函数f(x)=x图象上的任一点M,在函数g(x)=lnx上都存在点N(x0,y0),使以线段MN为直径的圆都经过坐标原点O,则x0必然在下面哪个区间内?( )| A. | ($\frac{1}{{e}^{3}}$,$\frac{1}{{e}^{2}}$) | B. | ($\frac{1}{{e}^{2}}$,$\frac{1}{e}$) | C. | ($\frac{1}{e}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
分析 以线段MN为直径的圆都经过坐标原点O,可得xx0+xlnx0=0,构造g(x)=x+lnx,可得g($\frac{1}{2}$)<0,g(1)>0,即可得出结论.
解答 解:设M(x,x),则
∵以线段MN为直径的圆都经过坐标原点O,
∴xx0+xlnx0=0,
∴x0+lnx0=0,
构造g(x)=x+lnx,可得g($\frac{1}{2}$)<0,g(1)>0,
∴x0∈($\frac{1}{2}$,1),
故选D.
点评 本题考查函数的性质,考查函数的零点,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.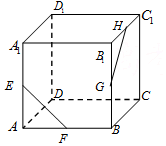 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
16.若函数$f(x)=\frac{2}{3}{x^3}-2{x^2}+ax+10$在区间[-1,4]上单调递减,则实数a的取值范围是( )
| A. | (-∞,-16]∪[2,+∞) | B. | (-16,2) | C. | [2,+∞) | D. | (-∞,-16] |
13.已知△ABC中,A:B:C=1:1:4,则a:b:c等于( )
| A. | 1:1:$\sqrt{3}$ | B. | 2:2:$\sqrt{3}$ | C. | 1:1:2 | D. | 1:1:4 |
14.已知函数f(x)对任意的x,y∈R都有f(x+y)=f(x)+f(y),且f(2)=4,则f(1)=( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |