题目内容
7.已知两点A(-m,0)和B(2+m,0)(m>0),若在直线l:x+$\sqrt{3}$y-9=0上存在点P,使得PA⊥PB,则实数m的取值范围是( )| A. | (0,3) | B. | (0,4) | C. | [3,+∞) | D. | [4,+∞) |
分析 以AB为直径的圆的方程为:(x-1)2+y2=(1+m)2.在直线l:x+$\sqrt{3}$y-9=0上存在点P,使得PA⊥PB,则直线l与圆有公共点.利用圆心到直线的距离与半径的关系即可得出.
解答 解:以AB为直径的圆的方程为:(x-1)2+y2=(1+m)2.圆心是(1,0)
在直线l:x+$\sqrt{3}$y-9=0上存在点P,使得PA⊥PB,则直线l与圆有公共点.
∴$\frac{|1-9|}{2}$≤1+m,解得m≥3.
故选:C.
点评 本题考查了直线与圆的位置关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.直线$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.(t$为参数)与圆$\left\{\begin{array}{l}x=4+2cosφ\\ y=2sinφ\end{array}\right.(φ$为参数)相切,则此直线的倾斜角$α({α>\frac{π}{2}})$等于( )
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
19.某几何体的三视图如图所示,则该几何体中最长的棱长为( )
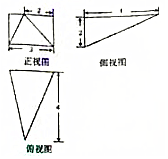

| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
16.某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
表1
表2
已知表1数据的中位数估计值为26,回答以下问题.
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线$\hat y=\hat bx+\hat a$的斜率和截距的最小二乘估计分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.)
表1
| 停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 频数 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线$\hat y=\hat bx+\hat a$的斜率和截距的最小二乘估计分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.)
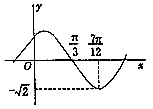 (1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;
(1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;