题目内容
若Sn是等差数列{an}的前n项和，且S8-S4=12，则S12的值为（ ）
| A、22 | B、36 | C、44 | D、64 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由已知得a1+a12=6，由此能求出S12的值．
解答：
解：∵S8-S4=a5+a6+a7+a8=12，
∴4a1+22d=12，
∴a1+（a1+11d）=6，
∴a1+a12=6，
∴S12=
(a1+a12)=6×6=36．
故选：B．
∴4a1+22d=12，
∴a1+（a1+11d）=6，
∴a1+a12=6，
∴S12=
| 12 |
| 2 |
故选：B．
点评：本题考查等差数列的前12项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
已知集合M={x|
≤1}，N={x|y=lg（1-x）}，则下列关系中正确的是（ ）
| 1 |
| x |
| A、（∁RM）∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、（∁RM）∪N=R |
已知等比数列{an}的首项为
，公比为-
，其前n项和为Sn，则Sn的最大值为（ ）
| 3 |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式x2-2x-3＞0的解集是（ ）
| A、（-1，3） |
| B、（3，+∞） |
| C、（-∞，-1）∪（3，+∞） |
| D、（-∞，-1） |
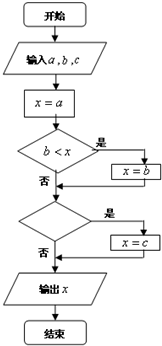如图所示程序框图中，如果输入三个实数a、b、c，要求输出这三个数中最小的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）| A、c＜x | B、x＜c |
| C、c＜b | D、b＜c |
已知集合A={-1，0，1}，B={x|-1＜x≤1}，则A∩B=（ ）
| A、{0} | B、{-1，0} |
| C、{0，1} | D、{1} |
若从区间（0，e）内随机取两个数，则这两个数之积不小于e的概率为（ ）
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|