题目内容

4．若圆锥的底面与顶点都在球O的球面上，且圆锥的底面半径为1，体积为π，则球O的表面积为（　　）
A．$\frac{16π}{9}$B．$\frac{100π}{9}$C．25πD．36π

分析 先求出圆锥的高，再利用射影定理，求出R，即可求出球O的表面积．

解答 解：设圆锥的高为h，球O的半径为R，则$\frac{1}{3}π×1×h$=π，
∴h=3，
由射影定理可得1=3×（2R-3），
∴R=$\frac{5}{3}$，
∴球O的表面积为4$π•\frac{25}{9}$=$\frac{100π}{9}$．
故选：B．

点评 本题考查球O的表面积，考查学生的计算能力，正确求出球O的半径是关键．

练习册系列答案
相关题目
14．已知数列{an}的前n项和Sn=3n2-n，bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$
（1）求数列{an}的通项公式；
（2）求数列{bn}的前n项和Tn．
15．法国数学家棣莫弗，A．（De Moivre，Abraham）证明了这样一个结论（也称棣莫弗定理）（cosα+isinα）n=cos（nα）+isin（nα）（这里i为虚数单位，n为正整数），应用此结论求下面式子的值
${C}_{7}^{0}$（cos$\frac{π}{7}$）7-${C}_{7}^{2}$（cos$\frac{π}{7}$）5（sin$\frac{π}{7}$）2+${C}_{7}^{4}$（cos$\frac{π}{7}$）3（sin$\frac{π}{7}$）4-${C}_{7}^{6}$（cos$\frac{π}{7}$）（sin$\frac{π}{7}$）6=-1．
12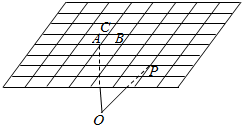．如图所示，已知A，B，C三点不共线，P为一定点，O为平面ABC外任意一点，则下列能表示向量$\overrightarrow{OP}$的为（　　）
A．$\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$B．$\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$C．$\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$D．$\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$
19．已知函数f（x）=lg（$\sqrt{{x}^{2}+2}$+x）-lg$\sqrt{2}$．
（1）判断函数f（x）的奇偶性；
（2）判断并用定义证明函数f（x）的单调性；
（3）若f（k•3x）+f（3x-9x-2）＜0对任意x∈R恒成立，求实数k的取值范围．
9．已知平行六面体ABCD-A′B′C′D′，则下列四式中：
①$\overrightarrow{AB}$-$\overrightarrow{CB}$=$\overrightarrow{AC}$；
②$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{B′C}$+$\overrightarrow{CC′}$；
③$\overrightarrow{AA′}$=$\overrightarrow{CC′}$；
④$\overrightarrow{AB}$+$\overrightarrow{BB′}$+$\overrightarrow{BC}$+$\overrightarrow{C′C}$=$\overrightarrow{AC}$．
正确的序号是①②③④．
16．已知点A（1，2），B（3，1），则过AB中点垂直于直线x+y+1=0的方程是2x-2y-1=0．
13．计算：已知sinα+2cosα=0，求$\frac{sin（\frac{3}{2}π-α）-2cos（\frac{3}{2}π+α）}{cos（π-α）+sin（π+α）}$的值．
18．一个椭圆的半焦距为2，离心率e=$\frac{2}{3}$，则它的短轴长是（　　）
A．3B．$\sqrt{5}$C．2$\sqrt{5}$D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网