题目内容
14.已知数列{an}的前n项和Sn=3n2-n,bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn.
分析 (1)由数列的前n项和求得首项,再由an=Sn-Sn-1(n≥2)求出数列通项公式;
(2)把数列{an}的通项公式代入bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$,然后利用裂项相消法求得数列{bn}的前n项和Tn.
解答 解:(1)由Sn=3n2-n,得a1=S1=2;
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=(3{n}^{2}-n)-[3(n-1)^{2}-(n-1)]$
=6n-4.
a1=2适合上式,
∴an=6n-4;
(2)由bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$=$\frac{\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}}}{{a}_{n+1}-{a}_{n}}=\frac{1}{6}(\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}})$,
∴Tn=b1+b2+…+bn=$\frac{1}{6}(\sqrt{{a}_{2}}-\sqrt{{a}_{1}}+\sqrt{{a}_{3}}-\sqrt{{a}_{2}}+…+\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}})$
=$\frac{1}{6}(\sqrt{{a}_{n+1}}-\sqrt{{a}_{1}})=\frac{1}{6}(\sqrt{6n+2}-\sqrt{2})$.
点评 本题考查数列递推式,训练了利用裂项相消法求数列的通项公式,是中档题.

练习册系列答案
相关题目
5.已知i是虚数单位,m,n∈R,则“m=n=1”是“m2-1-2ni=-2i”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.函数y=$\frac{ln(x+1)}{{\sqrt{{3^x}-27}}}$的定义域为( )
| A. | (-1,+∞) | B. | (-1,3) | C. | (3,+∞) | D. | [3,+∞) |
9.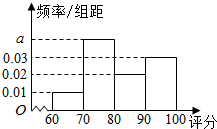 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
(1)求出频率分布与直方图中a的值;
(2)估计这200个零件评分结果的平均数和中位数;
(2)根据已有的经验,可能被修复的零件个体被修复的概率如表:
假设每个零件被修复与否相互独立.现有5个零件的检测指标评分结果为(单位:分):38,43,45,52,58,
①求这5个零件中,至多有2个不被修复而淘汰的概率;
②记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.
 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.(1)求出频率分布与直方图中a的值;
(2)估计这200个零件评分结果的平均数和中位数;
(2)根据已有的经验,可能被修复的零件个体被修复的概率如表:
| 零件评分结果所在区间 | (40,50] | (50,60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
①求这5个零件中,至多有2个不被修复而淘汰的概率;
②记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.
3.空间四边形ABCD中,M、G分别是BC、CD的中点,则$\overrightarrow{MG}$-$\overrightarrow{AB}$+$\overrightarrow{AD}$等于( )
| A. | $\frac{3}{2}$$\overrightarrow{DB}$ | B. | 3$\overrightarrow{MG}$ | C. | 3$\overrightarrow{GM}$ | D. | 2$\overrightarrow{MG}$ |
4.若圆锥的底面与顶点都在球O的球面上,且圆锥的底面半径为1,体积为π,则球O的表面积为( )
| A. | $\frac{16π}{9}$ | B. | $\frac{100π}{9}$ | C. | 25π | D. | 36π |