已知平行六面体ABCD-A′B′C′D′.则下列四式中:①$\overrightarrow{AB}$-$\overrightarrow{CB}$=$\overrightarrow{AC}$,②$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{B′C}$+$\overrightarrow{CC′}$,③$\overrightarrow{A 题目和参考答案——青夏教育精英家教网——

题目内容

9．已知平行六面体ABCD-A′B′C′D′，则下列四式中：
①$\overrightarrow{AB}$-$\overrightarrow{CB}$=$\overrightarrow{AC}$；
②$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{B′C}$+$\overrightarrow{CC′}$；
③$\overrightarrow{AA′}$=$\overrightarrow{CC′}$；
④$\overrightarrow{AB}$+$\overrightarrow{BB′}$+$\overrightarrow{BC}$+$\overrightarrow{C′C}$=$\overrightarrow{AC}$．
正确的序号是①②③④．

分析作出图形，结合图形利用向量的加减法进行化简判断．

解答解：①$\overrightarrow{AB}$-$\overrightarrow{CB}$=$\overrightarrow{AB}+\overrightarrow{BC}$=$\overrightarrow{AC}$，故①正确；
②$\overrightarrow{AB}$+$\overrightarrow{B′C}$+$\overrightarrow{CC′}$=$\overrightarrow{A′B′}$+$\overrightarrow{B′C}$+$\overrightarrow{CC′}$=$\overrightarrow{A′C′}$=$\overrightarrow{AC}$，故②正确；
③$\overrightarrow{AA′}$=$\overrightarrow{CC′}$，故③正确；
④$\overrightarrow{AB}$+$\overrightarrow{BB′}$+$\overrightarrow{BC}$+$\overrightarrow{C′C}$=$\overrightarrow{AB}+\overrightarrow{BB′}+\overrightarrow{B′C′}+\overrightarrow{C′C}$=$\overrightarrow{AC}$，故④正确．
故答案为①②③④．

点评本题考查了空间向量的加减运算及其几何意义，是基础题．

练习册系列答案

智能训练练测考系列答案

帮你学小学毕业总复习系列答案

课时导学案天津科学技术出版社系列答案

小学数学口算心算天天练系列答案

小学毕业升学模拟试题精选系列答案

单元测评卷对接中考系列答案

计算高手系列答案

实验报告册江苏人民出版社系列答案

小学毕业总复习归类卷系列答案

精编全程达标压轴卷系列答案

相关题目

19．设{a_n}为等差数列，S_n表示前n项之和，其中a₁+a₂=0，且S₃=3，求该数列的通项公式．

20．（1）函数y=lg（3-4x+x²）的定义域为A，当x∈A时，求f（x）=2^x+2-3×4^x的最值．
（2）已知函数f（x）=log_0.5（x²-ax-a）的值域为R，且f（x）在（-∞，1-$\sqrt{3}$）上是增函数，求a的取值范围．

17．求下列圆的方程：
（1）已知点A（-4，-5），B（6，-1），以线段AB为直径的圆的方程．
（2）过两点C（-1，1）和D（1，3），圆心在x轴上的圆的标准方程．

4．若圆锥的底面与顶点都在球O的球面上，且圆锥的底面半径为1，体积为π，则球O的表面积为（　　）

$\frac{16π}{9}$

$\frac{100π}{9}$

14．设集合M={y|y=2^x，x∈R}，N={x|y=log_a（x+1），a＞0，a≠1}，则M和N的关系是（　　）

1．对于每一个实数x，设f（x）是4x+1，x+2和4-2x三个函数中的最小值，则f（x）的最大值是（　　）

2．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，以坐标原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{6}$=0相切．
（1）求椭圆C的标准方程；
（2）设点P（4，0），A，B是椭圆C上关于x轴对称的任意两个不同的点，连结PB交椭圆C于另一点E，证明：直线AE与x轴相交于定点．

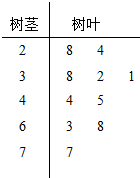我国政府对PM2.5采用如下标准：某市环保局从一年365天的市区PM2.5监测数据中，随机抽取10天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．

PM2.5日均值m（微克/立方米）	空气质量等级
m＜35	一级
35≤m≤75	二级
m＞75	超标

（1）求这10天数据的中位数；
（2）从这10天数据中任取4天的数据，记ξ为空气质量达到一级的天数，求ξ的分布列和期望；
（3）以这10天的数据来估计这一年365天的空气质量情况，并假定每天之间的空气质量相互不影响．记η为这一年中空气质量达到一级的天数，求η的平均值．