题目内容
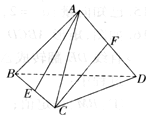
3.在三棱锥A-BCD中,E、F分别是AB,CD的中点,若AD=BC=2,AD与BC所成的角为θ,EF=$\sqrt{3}$,则sinθ=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 取BD的中点G,连结EG、FG,则EG∥AD,FG∥BC,从而∠EGF是θ(或θ的补角),由此利用余弦定理能求出sinθ.
解答 解:如图,取BD的中点G,连结EG、FG,
∵E、F分别是AB,CD的中点,
∴EG∥AD,FG∥BC,
∵AD=BC=2,AD与BC所成的角为θ,EF=$\sqrt{3}$,
∴∠EGF是θ(或θ的补角),
∴在△EFG中,EG=FG=1,EF=$\sqrt{3}$,
∴cos∠EGF=$\frac{E{G}^{2}+F{G}^{2}-E{F}^{2}}{2EG•FG}$=$\frac{1+1-3}{2}$=-$\frac{1}{2}$,
∴sinθ=$\sqrt{1-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题考查异面直线所成角的正弦值、余弦定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是基础题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
11.设向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=3,|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ,则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|cosθ}$+$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|cosθ}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{5}{4}$ | D. | 3 |
18.已知在△ABC中,角A,B,C所对的边分别为a,b,c,若C=2A,c=$\sqrt{3}$a,则$\frac{b}{a}$等于( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 1或2 |
8. 如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )
如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )
 如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )
如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
12.等差数列{an}中,a2+a8-a12=0,a14-a4=2,记sn=a1+a2+…+an,则s15的值为( )
| A. | 30 | B. | 56 | C. | 68 | D. | 78 |
 如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且$\overrightarrow{AE}=λ\overrightarrow{AB},\overrightarrow{AF}=μ\overrightarrow{AC}$,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则$\overrightarrow{MN}$的最小值为$\frac{\sqrt{7}}{7}$.
如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且$\overrightarrow{AE}=λ\overrightarrow{AB},\overrightarrow{AF}=μ\overrightarrow{AC}$,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则$\overrightarrow{MN}$的最小值为$\frac{\sqrt{7}}{7}$.