题目内容
19.设点O、P、Q是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与抛物线y2=4x的交点,O为坐标原点,若△OPQ的面积为2,则双曲线的离心率为$\sqrt{5}$.分析 求得双曲线的渐近线方程,联立求得P和Q点坐标,根据三角形的面积公式,即可求得$\frac{b}{a}$=2,由双曲线的离心率公式,即可求得双曲线的离心率.
解答 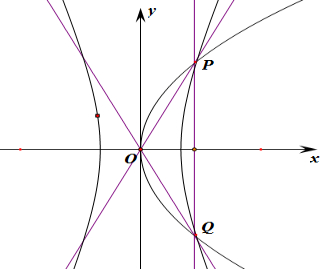 解:∵双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
解:∵双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
∴双曲线的渐近线方程是y=±$\frac{b}{a}$x,
则$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{{y}^{2}=4x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{2a}{b}}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$,
则P($\frac{2a}{b}$,2),同理求得Q($\frac{2a}{b}$,2),
△OPQ的面积为S=$\frac{1}{2}$×丨PQ丨×$\frac{2a}{b}$=2,则$\frac{b}{a}$=2,
∴双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{5}$,
双曲线的离心率$\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 本题考查双曲线的简单几何性质,直线与抛物线的位置关系,考查计算能力,属于中档题.

练习册系列答案
相关题目
9.若复数z=(sinα-$\frac{1}{3}$)+i(cosα-$\frac{2\sqrt{2}}{3}$)是纯虚数(i是虚数单位),则tanα的值为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | -$\frac{\sqrt{2}}{4}$ | C. | 2$\sqrt{2}$ | D. | -2$\sqrt{2}$ |
10.函数$f(x)={sin^2}x+\sqrt{3}sinxcosx$的一条对称轴为( )
| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=\frac{5π}{12}$ |
7. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )
 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
14.已知i为虚数单位,复数z满足z(1-i)=3+2i,则z=( )
| A. | $\frac{1}{2}$+$\frac{5i}{2}$ | B. | -$\frac{1}{2}$-$\frac{5i}{2}$ | C. | $\frac{5}{2}$+$\frac{5i}{2}$ | D. | -$\frac{5}{2}$-$\frac{5i}{2}$ |
4.设全集U={x|ex>1},函数f(x)=$\frac{1}{{\sqrt{x-1}}}$的定义域为A,则∁UA为( )
| A. | (0,1] | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
11.已知复数z=$\frac{a+i}{2i}$(其中i为虚数单位)的虚部与实部相等,则实数a的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | $-\frac{1}{2}$ |
3.在三棱锥A-BCD中,E、F分别是AB,CD的中点,若AD=BC=2,AD与BC所成的角为θ,EF=$\sqrt{3}$,则sinθ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |