题目内容
8.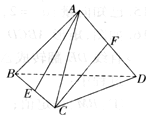 如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )
如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
分析 连接BF、EF,推导出AD⊥面BCF,AE在平面BCF上的射影为EF,设异面直线AE和CF所成的角为θ,则cosθ=cos∠AEF•cos∠EFC,由此能求出结果.
解答 解:连接BF、EF,
∵正四面体ABCD中,E、F分别是棱BC和AD的中点,
∴BF⊥AD,CF⊥AD,
又BF∩CF=F,∴AD⊥面BCF,
∴AE在平面BCF上的射影为EF,
设异面直线AE和CF所成的角为θ,正四面体棱长为1,
则$AE=CF=\frac{{\sqrt{3}}}{2}$,$EF=\frac{{\sqrt{2}}}{2}$.
∵cosθ=cos∠AEF•cos∠EFC,
∴cosθ=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}×\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{2}{3}$.
故直线AE和CF所成的角的余弦值为$\frac{2}{3}$.
故选:B.
点评 本题考查异面直线所成角的余弦值的求法,考查正四面体、线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设全集U={x|ex>1},函数f(x)=$\frac{1}{{\sqrt{x-1}}}$的定义域为A,则∁UA为( )
| A. | (0,1] | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
16.已知抛物线C:y2=8x的焦点为F,过F的直线l与抛物线C交于M(x1,y1),N(x2,y2)两点,若|MN|=8,则( )
| A. | x1+x2=8 | B. | x1+x2=4 | C. | y1+y2=8 | D. | y1+y2=4 |
3.在三棱锥A-BCD中,E、F分别是AB,CD的中点,若AD=BC=2,AD与BC所成的角为θ,EF=$\sqrt{3}$,则sinθ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
13.三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在A1B1上,且满足|A1P|=λ|A1B1|,直线PN与平面ABC所成角θ的正切值取最大值时λ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{5}}{5}$ |
20.已知函数f(x)=$\left\{\begin{array}{l}{-(x+1)•{e}^{x},x≤a}\\{bx-1,x>a}\end{array}\right.$,若函数f(x)有最大值M,则M的取值范围是( )
| A. | ($-\frac{1}{2}-\frac{1}{2{e}^{2}}$,0) | B. | (0,$\frac{1}{{e}^{2}}$] | C. | (0,$\frac{1}{2}+\frac{1}{2{e}^{2}}$] | D. | ($\frac{1}{2{e}^{2}}-\frac{1}{2}$,$\frac{1}{{e}^{2}}$] |
