Question

7．已知圆C₁：x²+y²-2ax+a²-1=0和圆C₂：x²+y²-2by+b²-4=0恰有三条公共切线，则$\sqrt{（a-3）^{2}+（b-4）^{2}}$的最小值为（　　）

• A． 1+$\sqrt{2}$
• B． 2
• C． 3-$\sqrt{2}$
• D． 4

Answer 1

分析 求出两圆的半径和圆心，根据两圆外切得出a，b的关系，根据几何意义得出最小值．

解答 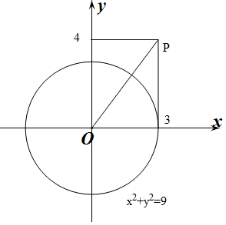解：圆C₁的圆心为C₁（a，0），半径为r₁=1，
圆C₂的圆心为C₂（0，b），半径为r₂=2，
∵两圆有三条公共切线，∴两圆外切．
∴$\sqrt{{a}^{2}+{b}^{2}}$=3，
∴点（a，b）在半径为3的圆x²+y²=9上．
而$\sqrt{（a-3）^{2}+（b-4）^{2}}$表示点（a，b）到点（3，4）的距离．
∴$\sqrt{（a-3）^{2}+（b-4）^{2}}$的最小值为$\sqrt{{3}^{2}+{4}^{2}}$-3=2．
故选B．

点评 本题考查了圆与圆的位置关系，距离公式的应用，属于中档题．